Questão 1, UFF, P1-2016.1
A figura abaixo mostra um ciclo que de gás monoatômico ideal sofre. As temperaturas são
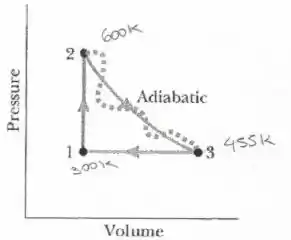
Para os processos
- Calcule
- Calcule a de através da trajetória pontilhada, indicada na figura.
Para todo o ciclo, calcule:
Passo 1
a)
Vamos calcular para cada processo:
A transformação acontece a volume constante, assim não há realização de trabalho:
Só precisamos calcular o calor, então:
Assim:
Esse é um processo adiabático. Assim:
A variação da energia interna pode ser calculada por:
E assim:
Temos uma compressão isobárica.
O calor é dado por:
E a energia interna:
Assim, o trabalho:
Assim:
Passo 2
b)
O calor total do ciclo é a soma dos calores:
Como a variação de energia interna de um ciclo é nula:
Temos:
Assim:
Passo 3
c)
Essa é uma questão meio pegadinha: Como sabemos a energia interna não depende do caminho do processo, e sim dos pontos inicial e final. Assim, a variação da energia interna vai ser exatamente a mesma que a anteriormente calculada:
Resposta
a)
b)
c)