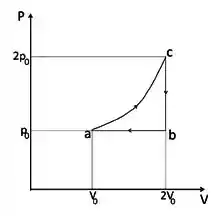
Um mol de um gás ideal ( ) é submetido a um ciclo termodinâmico reversível, como mostra a figura ao lado. No processo não especificado ab, a variação de energia interna vale e o calor absorvido neste tempo é de . Determine:
a) O trabalho realizado no ciclo.
b) A eficiência do ciclo.
c) A variação de entropia do gás no processo ca em termos de R. Analisando sua resposta, explique a validade da segunda lei da termodinâmica usando o conceito de subsistemas em processos reversíveis.
Passo 1
a) Vamos aplicar a 1ᵃ Lei da Termodinâmica no processo ab:
O trabalho total no ciclo vai ser:
E do gráfico conseguimos ver que:
E:
O trabalho em ba podemos calcular pela área do gráfico:
Então:
O trabalho total então vai ser:
Passo 2
b) O único processo que o ciclo recebe calor é o ab! Então o rendimento vai ser:
Passo 3
c) Aqui vamos usar a 1ᵃ Lei da Termodinâmica na forma infinitesimal:
Como:
Passo 4
Como:
Vamos trocar na segunda integral:
E podemos usar pra achar a relação entre os volumes e as temperaturas:
E trocando:
De acordo com a 2ᵃ Lei da Termodinâmica, a variação de entropia sempre deve ser maior ou igual a zero. Aqui tá dando um número negativo! Isso acontece porque o nosso gás é só um subsistema de um sistema grandão. Nos outros subsistemas, ou seja: nas vizinhanças do gás, a variação de entropia vai ser positiva. E aí a variação de entropia total, somada com a do gás, vai dar zero. Como deve ser em um processo REVERSÍVEL.
Resposta
a)
b)
c)