Um mol de gás ideal formado por moléculas diatômicas (que giram, mas não oscilam) é submetido a um ciclo fechado que passa pelos estados . O ciclo é composto pelas três etapas descritas abaixo.
: Expansão adiabática com trabalho realizado .
: Compressão isotérmica a uma temperatura .
: Aumento de pressão a volume constante até voltar ao estado inicial.
a)Esboce as três etapas do ciclo em um diagrama .
b)Determine a temperatura do sistema no estado (ou seja, imediatamente antes da expansão adiabática). Use
c)Calcule a eficiência de uma máquina térmica operando segundo esse ciclo. [Dica: utilize a relação entre as temperaturas e os volumes final e inicial em um processo adiabático para obter a razão entre os volumes envolvidos no ciclo e use a aproximação .
Passo 1
- Temos uma expansão adiabática, uma isotérmica e uma isovolumétrica. Assim, teremos duas curvas e uma reta inclinada(
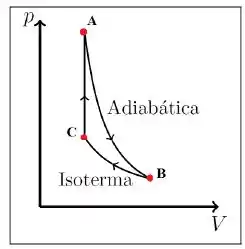
Passo 2
b)
Como a transformação é adiabática, podemos dizer que:
Só que é dado por:
Quanto vale ? Como é um gás diatômico:
Assim:
Quanto vale ? Como ocorre uma transformação isotérmica envolvendo , a temperatura será:
Assim:
Passo 3
c)
Precisamos calcular os calores trocados pelo sistema. Primeiro, vamos calcular no processo
E o calor
Como o processo é isotérmico:
Assim:
Podemos chamar de:
Assim:
Como ( eles estão unidos por uma isovolumétrica) então:
Mas qual a relação entre os volumes final e inicial? Bom, eles estão conectados por uma adiabática, certo? Então podemos usar:
Assim:
Como o gás é diatômico:
Assim:
Passo 4
O calor trocado com a fonte quente é o calor positivo:
E o rocado com a fonte fria o calor negativo:
Assim, a eficiência será:
Resposta
a)
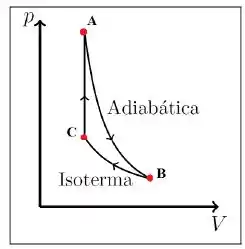
b)
c)