Um mol de um gás monoatômico ideal realiza o ciclo mostrado na figura. O processo é uma contração isotérmica reversível. São conhecidos e e sabe-se que e .
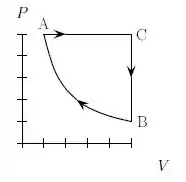
Supondo conhecidas as relações entre , , R e o número de graus de liberdade do gás, o trabalho líquido feito pelo o gás no ciclo pode ser escrito como:
(a)
(b)
(c)
(d)
(e)
Passo 1
O trabalho no ciclo é igual à área do gráfico! Então podemos dizer que:
Mas, perceba que o trabalho realizado de B para A será negativo!! Pois é uma contração isotérmica. Só que a área debaixo da curva de B para A não tem área negativa... Portanto, o que faremos aqui é considerar os módulos das áreas:
Beleza?? Senão acabaríamos somando as duas áreas (ficaria ) e não é o que queremos.
Show! Então só precisamos calcular esses dois trabalhos né? Então vamos lá!
Passo 2
Vamos calcular o trabalho em AC:
Show!
Passo 3
Agora vamos calcular o trabalho em BA:
Mas ele disse que:
E pelo gráfico:
Então:
Sabemos que , então só falta calcular a temperatura no processo BA.
Passo 4
Ou:
Você poderia usar qualquer um dos dois! Vou usar os valores de A:
Vamos trocar lá no trabalho:
Passo 5
O trabalho no ciclo vai ser então:
Resposta
Letra E.