A figura representa um processo termodinâmico sofrido por de hélio.
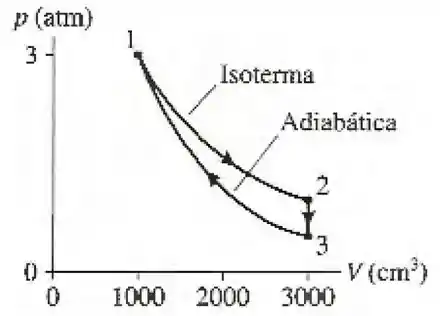
Determine a pressão (em ), a temperatura (em ) e o volume (em ) do gás correspondentes aos pontos , e . Disponha seus resultados em uma tabela para facilitar a leitura.
Quanto trabalho é realizado sobre o gás durante cada um dos três segmentos mostrados na figura?
Quanto calor é transferido para o gás ou para fora dele durante cada um dos três segmentos?
Passo 1
Para resolver o item , vamos utilizar a famosa lei dos Gases Ideais:
Mas, precisamos primeiro determinar o número de mols envolvido!
Vamos agora reunir os dados que temos a respeito do ponto :
Portanto, precisamos determinar a temperatura , para isso, é só substituir na fórmula!
Vamos agora para o ponto ! Por se tratar de um processo isotérmico, temos que :
Agora é só substituir na fórmula para determinar a pressão , temos então:
Para o ponto , temos que ocorre um processo adiabático de para , desse modo, temos:
Isolando a pressão , que queremos determinar, temos:
Por se tratar de um gás monoatômico, temos:
Substituindo os dados, temos:
Para a temperatura , temos:
Dispondo os resultados em uma tabela, temos:

Passo 2
De para , por se tratar de um processo isotérmico, temos que a variação do trabalho é:
Substituindo os valores, temos:
De para , por se tratar de um processo isocórico, o trabalho é nulo!
De para , por se tratar de um processo adiabático, temos que a variação de trabalho é dada por:
Substituindo os valores, temos:
Passo 3
De para , por se tratar de um processo isotérmico, temos que a variação de energia interna é nula, portanto, temos:
De para , por se tratar de um processo isocórico, o trabalho é nulo, desse modo, temos:
De para , por se tratar de um processo adiabático, temos que:
Resposta

; ;
; ;