Uma quantidade de gás oxigênio (O2) é submetida a processos termodinâmicos do estado inicial até o estado final por duas trajetórias distintas e indicadas na figura. A temperatura no ponto é . O gráfico abaixo, à direita, mostra o calor específico molar do oxigênio em função da temperatura.
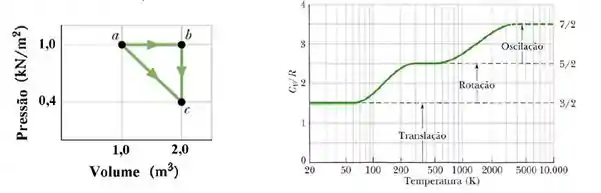
- Determine o número de moléculas por cm3 no estado inicial.
- a variação da energia interna do gás;
- o trabalho realizado pelo gás e a energia adicionada ao gás na forma de calor.
- o calor necessário para que o gás vá de até ao longo da trajetória .
No processo ac determine:
No processo abc determine:
Passo 1
Inicialmente temos que fazer algumas considerações, por exemplo: Vamos supor que estamos trabalhando com um gás ideal e, para isso, podemos considerar que o gás oxigênio pode ser descrito pela equação de Clapeyron:
Vamos de fato ao exercício agora. Estamos interessados em saber o número de moléculas por no estado inicial (. Então podemos escrever a equação de Clapeyron como:
Passo 2
Pessoal quando a gente quer calcular a variação da energia interna do gás , devemos utilizar da primeira lei da termodinâmica:
Analisando o gráfico na , encontramos o valor correspondente de . Logo:
Passo 3
Agora vamos calcular o trabalho realizado pelo gás e a energia recebida pelo gás na forma de calor. Bora lá!
O trabalho total pode ser calculado pela área formada pelo gráfico :
Já o calor recebido pelo gás, é calculado da forma:
Passo 4
Analogamente ao passo anterior, temos que:
Rearranjando os termos da equação:
Resposta
- -