Um mol de um gás ideal diatômico é submetido ao processo termodinâmica descrito a seguir:
I – O gás, inicialmente à uma pressão ocupando um volume , passa por um processo adiabático até que sua pressão seja reduzida à metade.
II – Em seguida, é expandido até um volume , mantendo a pressão constante.
III – O gás é então comprimido isotermicamente até seu estado inicial.
Dados: ; .
Determine:
a) O volume do gás ao final do processo I.
b) A variação da energia interna do gás a partir do início do processo I até o final do processo II.
c) O trabalho total para o ciclo.
d) O coeficiente de desempenho para este ciclo.
Passo 1
Fala galerinha, nesse problema vamos brincar um pouco com ciclos termodinâmicos!
Para problemas desse tipo, é essencial fazer um diagrama representando todos os processos:
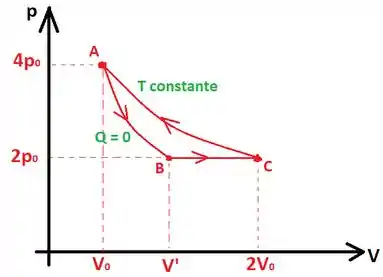
Observe que I é o processo , II é e III é .
No item (a) ele quer saber o volume do gás ao final do processo I, isto é, o volume no ponto , representado por . Como o processo é adiabático, vale a relação
Assim,
Usando e , temos que
Para um gás diatômico, temos que , de modo que
Como , segue que
Passo 2
No item (b) nós queremos a variação de energia interna entre o ponto e o ponto , passando pelo ponto :
Como a energia interna é uma função de estado, a soma das variações de todos os processos no ciclo deve ser zero:
Como o terceiro processo () é isotérmico, temos que . Assim,
Logo, a variação da energia interna entre o início do processo I e final do processo II é nula!
Passo 3
No item (c) ele pede para calcularmos o trabalho total no ciclo. Para isso, vamos calcular o calor e o trabalho em cada etapa.
Começando pela etapa I. Como é um processo adiabático, temos . Portanto, usando a segunda lei da termodinâmica:
Para um gás diatômico:
Assim,
Como :
Lembrando que :
Daí é só substituir:
Assim,
Passo 4
Já no processo II, temos que a pressão é constante, de modo que
Já para a variação da energia interna:
Logo,
Passo 5
Para fechar, vamos ao processo III. Como ele é isotérmico, temos , de modo que
Para calcular o trabalho, usamos
Assim,
Mas note também que
Logo,
Com isso, podemos calcular o trabalho total no ciclo somando todos os trabalhos:
Passo 6
No item (d) ele pergunta sobre o coeficiente de desempenho do ciclo. Esse coeficiente é a razão do calor da fonte fria pelo trabalho total:
Nesse ciclo, o calor da fonte fria corresponde ao calor negativo, o que é verificado no processo III:
Assim,
E com isso nós finalizamos o problema 😉.