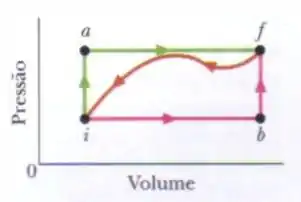
Quando um sistema passa do estado para o ao longo da trajetória da figura abaixo, . . Ao longo da trajetória , .
Quanto vale ao longo da trajetória ?
Se na trajetória de retorno , quanto vale nessa trajetória?
Se , qual o valor de ?
Se , qual o valor de na trajetória ?
Se , qual o valor de na trajetória
Passo 1
Bom, como a variação da energia interna não depende do caminho, podemos escrever:
No percurso
Logo:
Passo 2
Novamente, a variação da energia interna não depende do caminho. No entanto, a variação da energia interna deve ser negativa em relação aos percursos que vão de pra Então:
Passo 3
A gente pode escrever:
Com:
Logo:
Passo 4
Tendo o valor da energia interna de e de , a gente pode calcular a variação da energia interna e aplicar a primeira lei entre os dois pontos. A gente sabe o trabalho realizado nesse percurso, então fica fácil calcular o calor no mesmo:
Logo:
Bom o trabalho ali é o mesmo trabalho do percurso , logo:
Passo 5
Vamos fazer a mesma coisa que antes:
Como (transformação isovolumétrica), a equação fica:
Resposta