Seja a matriz que representa a projeção ortogonal na reta seguida da reflexão pela reta . Assinale os autovalores de
(a) apenas 1
(b) 1 e 0
(c) e 0
(d)e
Passo 1
Bom, primeiro eu tenho uma projeção ortogonal em uma reta, sabemos que os autovalores desse tipo de transformação são 1 e 0.
Isso porque se eu aplicar vetores pertencentes a reta , ou seja, aqueles cujas coordenadas são:
A transformação vai me retornar eles mesmos.
E se eu aplicar vetores perpendiculares a essa reta, , a projeção vai ser nula e portanto estão associados ao autovalor
Passo 2
Agora vamos ver o que acontece com esses autovetores quando aplicamos a segunda transformação.
Primeiramente, aqueles que foram levados a zero pela projeção, depois de refletidos pela reta vão continuar sendo zero! Assim, já provamos que é um autovalor dessa composição de transformações.
Passo 3
Agora os autovetores associados a vamos ver o que acontece com eles:
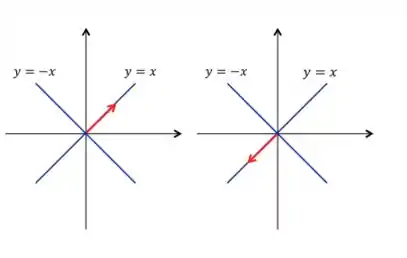
Opa, após a reflexão pela reta , a segunda transformação, o vetor pertencente a continua na mesma direção, apenas com sentido contrário! Logo, chegamos a conclusão que outro autovalor dessa composição de transformações é
Resposta
c