Sejam e transformações lineares de em , sendo injetiva e sobrejetiva. A única afirmativa que pode ser verdadeira é:

1. é a projeção ortogonal sobre .
2. é autovalor de .
3. é autovalor de .
4. é uma rotação em torno da reta

Na letra (a), ele tá afirmando que é a projeção ortogonal sobre . Mas é na projeção ortogonal que tá a malandragem, porque toda projeção ortogonal leva o vetor perpendicular à reta em questão no , isto é, seja o vetor perpendicular a , temos que:

Dessa maneira, teríamos que é um autovalor associado a , tal que:

Maaass, uma transformação injetiva, como , NÃO PODE ter o autovalor . Então isso seria uma inconsistência, que resulta na nossa alternativa (a) sendo Falsa.

Agora na letra (b) ele afirma que é autovalor de . E acabamos de ver no Passo 1, que uma função injetiva NÃO PODE ter um o autovalor . Isso ocorre porque uma função injetiva exige que a dimensão do núcleo seja igual a 0, ou seja, não pode haver nenhum vetor no núcleo da transformação tal que:

Mas quando se tem o autovalor , obrigatoriamente vai se ter também um autovetor associado a ele, e sempre, SEMPRE, o autovetor associado a vai estar no núcleo da transformação!!

Portanto nossa letra (b), também é Falsa.

E na nossa letra (c), ele diz que é autovalor de . E aqui precisamos lembrar que é uma transformação sobrejetiva

Uma função sobrejetiva, é aquela cujo a dimensão da imagem é igual a dimensão do contradomínio. Mas calma aí, porque nossa função é

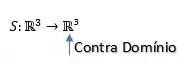
Então a dimensão do contradomínio é igual a , e em consequência disso:

E através do Teorema do Núcleo e Imagem, temos que:

Onde é igual a dimensão do DOMÍNIO. E se o contradomínio era o da direita:

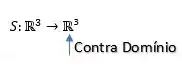
O domínio agora vai ser o da esquerda, que por coincidência também é igual a . Logo:

Então quer dizer que a , e dessa forma a transformação além de sobrejetiva, também vai ser injetiva. E como vimos no Passo 1 e 2, uma função injetiva, nunca, jamais, NEVER poderá ter o autovalor . Dessa forma a afirmativa (c) também é Falsa.

Bom só restou essa alternativa pra gente né rsrs

Então bora testar ela só pra ter certeza mermo! Ela tá dizendo pra gente que é uma rotação em torno da reta . Bom galerinha, se ela é uma rotação em torno da reta, quer dizer que ela rotaciona todos os vetores ortogonais a essa reta por um ângulo pré determinado, MAASSS uma rotação não consegue “levar” nenhum vetor na origem a não ser o próprio , isso quer dizer que a dimensão do núcleo de uma rotação sempre será , e a segunda propriedade é que uma transformação de rotação SEMPRE será sobrejetiva. E essas são propriedades que por coincidência combinam com , tornando possível ela ser uma rotação em torno da reta . Portanto, letra (d) é verdadeira.