Sejam e matrizes . Considere as seguintes afirmativas:
- Se não tem autovetores, então não tem autovetores.
- Mesmo que tenha apenas uma direção de autovetores, pode ter duas direções distintas de autovetores.
Ambas são verdadeiras
é falsa e é verdadeira
Ambas são falsas
é verdadeira e é falsa.
Passo 1
Afirmativa :
Vou te dar um exemplo pra provar que isso é falsa! Pega a matriz sendo a rotação de no sentido horário. Ela não tem autovetor nenhum concorda? Não preserva nenhuma direção! Agora pega sendo a matriz rotação de no sentido horário!
Fazendo nós estamos simplesmente rodando um vetor de e depois rodando de mais ! Logo, ele acaba rodando , voltando nele mesmo. Então todo vetor do seria autovetor de . Essa é falsa.
Passo 2
Afirmativa :
Um exemplo de matriz com apenas uma direção de autovetores é o cisalhamento lembra? Ele “tomba” o paralelogramo formado por um vetor, mantendo sua base e alturas inalteradas:
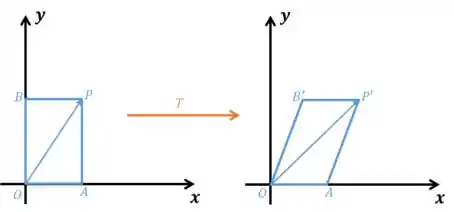
Nesse caso da imagem, a única direção que ele mantém inalterada é a dos vetores sobre o eixo . Logo, ele tem apenas uma direção de autovetores. Se não conseguiu ver, pode calcular o autovetor da matriz dele:
Beleza, essa vai ser nossa matriz . Se a gente definir como sendo a projeção sobre o eixo , temos que vai jogar todos os vetores em e por sua vez não vai fazer coisa nenhuma porque ela não mexe em vetores no eixo haha.
Logo, temos que nossa matriz vai fazer a mesma coisa que nossa matriz , que sabemos que possui duas direções de autovetores. Então também terá duas direções de autovetores.
Essa é verdadeira.
Resposta
Letra