UFRJ, Álgebra Linear, P3 – 2017.2, Questão 16
Sejam a projeção ortogonal no subespaço e a reflexão por
(a) Ambas são verdadeiras
(b) é falsa e é verdadeira
(c) Ambas são falsas
(d) é verdadeira e é falsa
Passo 1
Vamos pensar em um exemplo pra ficar mais fácil de pensar, vamos supor que é o eixo e estamos no , fazendo o ser o eixo
Vamos ver a primeira afirmativa:
Vamos analisar o primeiro lado da igualdade:
Aqui estamos pegando um vetor, o refletindo e depois o projetando infinitas vezes sobre o eixo Mas pensa aqui comigo, repetir infinitas vezes a projeção de um vetor num espaço, é o mesmo que fazer essa projeção apenas uma vez!
Isso acontece porque quando projetamos uma vez, o vetor passa a pertencer ao eixo Aí quando vamos projetar num espaço um vetor que pertence a ele, esse vetor permanence o mesmo!
Logo,
Passo 2
Agora vamos ver a outra parte da igualdade:
Aqui estamos pegando um vetor e o refletindo um número ímpar de vezes no eixo para depois o projetar no eixo . Acontece que refletir um número ímpar de vezes é igual a refletir apenas uma vez.
Isso acontece porque quando refletimos o vetor já refletido, ou seja, refletimos pela segunda vez, o vetor resultante é o inicial! Assim, quando fazemos a terceira reflexão, vai ser igual a primeira, e isso se repete por todos os numeros ímpares.
Logo,
Logo essa afirmativa é verdadeira!
Passo 3
Agora a afirmativa
Agora, no primeiro lado da igualdade, estamos refletindo o vetor em e o projetando em um número par de vezes:
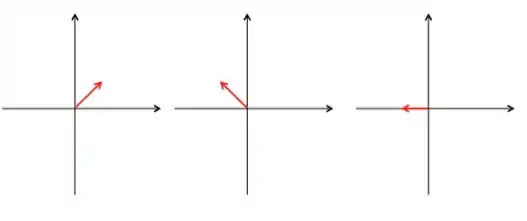
Peguei um vetor, refleti em e projetei em , agora vou fazer pela segunda vez:
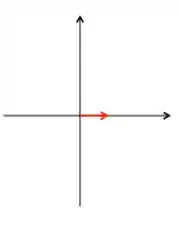
Refleti em e opa, ele já ta projetado em logo, continua o mesmo!! E só para entender o processo, vou fazer uma terceira vez:
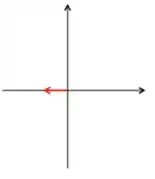
Acho que deu pra entender a ideia da coisa. Quando fazemos o processo um número par de vezes, o resultado é igual àquele encontrado quando feito 2 vezes. Já quando fazemos o processo um número ímpar de vezes, o resultado é igual ao que encontramos fazendo 1 vez ou 3 vezes!
Assim,
A afirmativa é negativa!
Resposta
d