Assinale a área do paralelogramo definido pelos pontos e:
- .
- .
- .
- .
Passo 1
Belezoca galerinha, queremos encontrar a área do paralelogramo forma pelos pontos:
Se a gente colocar isso num gráfico teríamos algo parecido com isso:
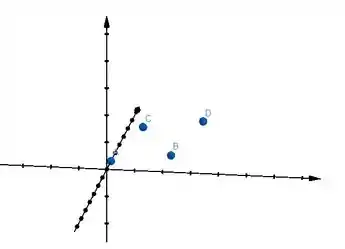
A gente pode perceber que de fato formamos um paralelogramo com esses pontos. Se a gente for desenho melhor somente o paralelogramo, ia ficar mais ou menos assim:
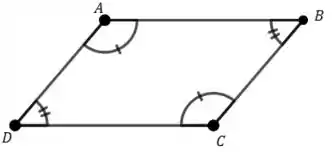
E colocando algumas informações importantes, temos o seguinte desenho:
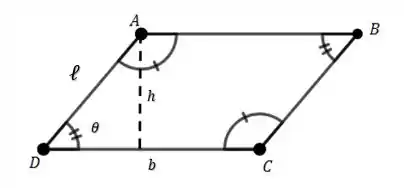
Onde é a altura desse paralelogramo, é a base e é o lado. Além disso, é o ângulo menor formado pelo lado e a base. E para um paralelogramo desses, a área é medida através da fórmula:
Então a gente só precisa encontrar essa tal base e essa tal altura que poderemos encontrar a área. Cola aqui comigo.

Passo 2
Belezoca galera, como temos apenas as coordenadas dos pontos, precisamos traçar os segmentos que ligam os pontos, esses segmentos vão ser os nossos lado e base. Então para o lado, temos o segmento , logo:
E seu módulo é:
E para a base, temos o segmento dado por:
Onde o módulo é:
Iradoso, então agora já temos os segmentos que formam os lados do nosso paralelogramo!!
Passo 3
Xuxu beleza então, agora a gente precisa encontrar a altura do paralelogramo. E pra isso, a gente pode usar algumas relações trigonométricas com ângulo . Saca só, na minha figura a gente tem o triângulo retângulo em vermelho:
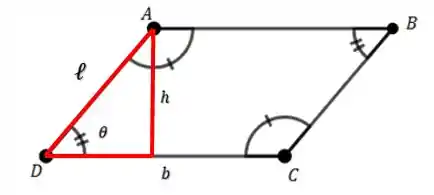
Então quer dizer que:
Logo, substituindo o módulo de que encontramos, temos que:

Mas calma lá chefe, porque agora que vem a malandragem. Não sabemos calcular o seno de um ângulo entre dois segmentos, MAAASSSSS sabemos calcular o cosseno do ângulo entre dois segmentos.

Sabemos siimm, e o método tem um nome muito chique, a chamada Desigualdade de Cauchy-Schwarz, que diz que o cosseno de um ângulo entre dois segmentos e , é dado por:
Mas no nosso caso, temos que esses segmentos e são o lado e a base e respectivamente, logo:
Então substituindo os valores que conhecemos, temos que:

E agora que vem a parte divertida, porque o seno e o cosseno de um ângulo se relacionam através da identidade fundamental:
Logo:
E substituindo tudo que encontramos, temos que:
Logo:

Passo 4
Então voltando pra problemática inicial da área, temos que ela ia ser dada por:
E encontramos que e logo:

Nossa resposta então é a alternativa (c), .
Resposta
Letra (c), .