Seja uma rotação em torno do eixo gerado por . Suponha que mande o vetor no vetor . Calcule o ângulo da rotação. (Sugestão: Utilize a projeção no plano perpendicular ao eixo de rotação)
graus
graus
graus
graus
Passo 1
Reparem o seguinte galera, quando estamos no e giramos um vetor, o ângulo de rotação é justamente o ângulo entre os dois vetores certo? Infelizmente, no , isso não é verdade!
Então o que nós podemos fazer pra resolver isso? Levar o problema para o plano!! Lá sabemos como resolvê-lo! E é exatamente isso que nos é sugerido. O ângulo de rotação será exatamente o ângulo entre as projeções do vetor inicial e do vetor rotacionado no plano perpendicular ao nosso eixo.
Ta difícil de visualizar? Vou te dar uma ajudinha:
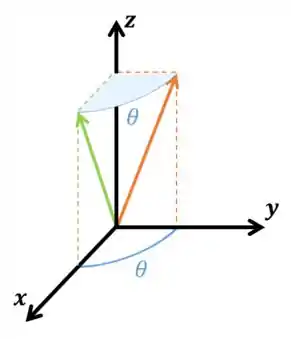
Eu botei o vetor girando em torno do eixo assim como no problema. Nesse caso dá pra ver que , mas dá pra perceber que serve pra qualquer âlgulo certo? Então primeiro temos que projetar os vetores e no plano e depois achar o ãngulo entre eles.
Passo 2
Por sorte, projetar no plano é muito fácil haha, basta zerarmos a coordenada do nosso vetor certo? Então:
E para calcular o ângulo entre eles usamos a fórmula:
Onde:
Então:
Os únicos ângulos das opções que possuem cosseno negativo são e . Mas como sabemos que , então a resposta só pode ser .
Passo 3
Tá, essa é a forma bonitinha de se fazer. Vou mostrar agora o jeito rápido que explora as opções! Repare que o vetor inicial tem coordenada e positivas e coordenada . Isso quer dizer que ele está entre o e o octantes (parte positiva do plano )!
Esse vetor é levado no vetor que possui coordenadas e positivas e coordenada negativa. Logo, ele se encontra no octante!
Pra um vetor passar da parte positiva do plano para o segundo octante ele precisa ser girado de um tal que:
Pois se ele girasse ele pararia entre o e octantes e se ele girasse ele pararia entre o e octantes. O único ângulo que está entre e é o então essa tem de ser a resposta!
Resposta
Letra