UFRJ, Álgebra Linear, P4 – 2017.1, Questão 8
Seja um conjunto ortonormal de . Seja o tetraedro cujas arestas são representadas por . Calcule a área da superfície de :
(a)
(b)
(c)
(d)
Passo 1
Esse vai ser meu conjunto ortonormal:
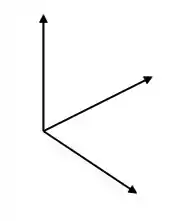
Vou achar agora os vetores :
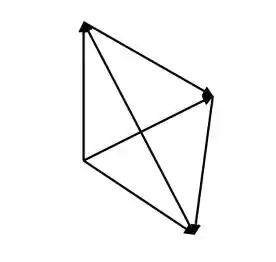
Ele pede a área da superfície e eu tenho 3 triângulos retângulos isósceles e um não retângulo equilátero de lado igual a (porque é a hipotenusa dos outros triângulos cujos lados são iguais a 1).
Passo 2
Aí é só somar todas essas áreas:
Triângulos retângulos:
Triângulo equilátero:
Somando:
Resposta
d
Exercícios de Livros Relacionados
Considere R 2 ,R 3 e R 4 com o produto interno euclidiano. Em cada parte, encontre o cosseno do ângulo entre u e v . u = 1 , - 3 , v = 2,4 u = - 1,0 , v = 3,8 u = - 1,5 , 2 , v = 2,4 , - 9 u = 4,1 , 8
13. Quais as condições devem satisfazer a e b para que a matriz a + b b - a a - b b + a seja ortogonal?
Dizemos que um operador matricial R 2 é rígido se mantiver o comprimento dos vetores, e preserva ângulo se não mudar o ângulo entre vetores não nulos.(a) Dê o nome de dois tipos distindos de operadore
O resultado do Exercício 15 tem um análogo para matrizes ortogonais 3 × 3 , como segue. Pode ser provado que a multiplicação ortogonal A de tamanho 3 × 3 é uma rotação em torno de algum eixo se d e t
7. Repita o Exercício 6 com theta = (pi)/(3) .