No paralelepípedo da figura, , , , . Calcule o comprimento da diagonal desse paralelepípedo que tem origem em .
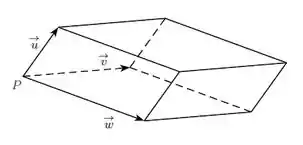
Passo 1
A diagonal desse paralelepípedo com origem em vai ser esse vetor vermelho que vamos chamar de :
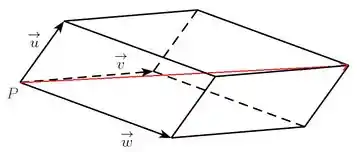
Esse vetor é dado por certo?
Então para acharmos o comprimento da diagonal, precisamos encontrar .
Vamos fazer isso encontrando e depois tirando a raíz quadrada do resultado :)
Passo 2
Vamos fazer os cálculos então:
Fazendo a distributiva:
Agrupando os vetores e aplicando a definição de produto interno (vamos lembrar que o ângulo entre e é o mesmo entre e ok?):
Vamos substituir os valores:
Resposta
Exercícios de Livros Relacionados
Considere R 2 ,R 3 e R 4 com o produto interno euclidiano. Em cada parte, encontre o cosseno do ângulo entre u e v . u = 1 , - 3 , v = 2,4 u = - 1,0 , v = 3,8 u = - 1,5 , 2 , v = 2,4 , - 9 u = 4,1 , 8
13. Quais as condições devem satisfazer a e b para que a matriz a + b b - a a - b b + a seja ortogonal?
Dizemos que um operador matricial R 2 é rígido se mantiver o comprimento dos vetores, e preserva ângulo se não mudar o ângulo entre vetores não nulos.(a) Dê o nome de dois tipos distindos de operadore
O resultado do Exercício 15 tem um análogo para matrizes ortogonais 3 × 3 , como segue. Pode ser provado que a multiplicação ortogonal A de tamanho 3 × 3 é uma rotação em torno de algum eixo se d e t
7. Repita o Exercício 6 com theta = (pi)/(3) .