Um átomo de hidrogênio , movendo-se com velocidade , colide elasticamente com uma molécula de hidrogênio em repouso, sofrendo uma deflexão de .
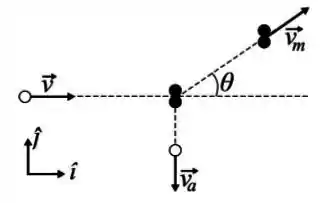
(a) Calcule o valor numérico do ângulo , em graus, da figura entre a direção do movimento da molécula após a colisão e a direção inicial de movimento do átomo.
(b) Calcule os módulos das velocidades do átomo e da molécula após a colisão em termos de .
Passo 1
a) Pela conservação do momento linear, temos que:
No eixo :
No eixo :
A colisão é elástica, portanto:
Mas:
Ficamos com o sistema
Organizando as equações acima, chegamos que:
Logo:
Usando a identidade fundamental, temos que:
Passo 2
b) Substituindo o valor de nas equações obtidas anteriormente, temos:
Resposta
a)
b) ,
Exercícios de Livros Relacionados
Uma bola de 8,0k g , suspensa do teto por um fio leve de 135c m de comprimento, é atingida em uma colisão elástica por uma bola de 2,0k g que se move horizontalmente a 5,0m / s imediatamente antes da
Uma bola de massa M que se move horizontalmente a 5,0m / s colide elasticamente com um bloco de massa 3 M , que está inicialmente suspenso em repouso do teto por um fio de 50,0c m . Ache o ângulo máxi
Na Fig. 9-69, o disco 1, de massa m 1=0,20k g , desliza sem atrito em uma bancada de laboratório até sofrer uma colisão unidimensional com o disco 2, inicialmente em repouso. O disco 2 é arremessado p
Uma pequena esfera de massa m está verticalmente acima de uma bola maior de massa M=0,63k g (com uma pequena separação, como no caso das bolas de beisebol e basquete da Fig.9 -68a) e as duas bolas são
As três bolas vistas de cima na Fig. 9-76 são iguais. As bolas 2 e 3 estão se tocando e alinhadas perpendicularmente à trajetória da bola 1. A velocidade da bola 1 tem módulo v 0=10 m / s e está dirig