As duas massas à direita, e conforme mostra figura abaixo, estão ligeiramente separadas e inicialmente em repouso; a massa da esquerda incide sobre as outras duas com velocidade . Supondo que as colisões sejam diretas e elásticas:
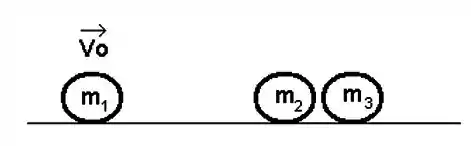
(a) Achar a velocidade que a segunda massa adquire. Considerar o choque elástico e frontal.
(b) Achar a velocidade que a última massa adquire.
(c) Mantendo e constantes, calcule o valor de para que a velocidade do terceiro corpo seja máxima.
Passo 1
(a)
No caso da colisão elástica temos a conservação do momento linear e da energia cinética. Assim:
Da equação (1) temos:
Substituindo em (2):
Passo 2
(b)
Analogamente, a bola 3 irá sofrer uma colisão elástica com a segunda e chegaremos na mesma equação que o item anterior:
Substituindo o :
Passo 3
(c)
Alterando o valor de , o valor de vai sendo alterado também, pois eles são dependentes pela equação que encontramos no item anterior. Como e são constantes, teremos uma função , cujo o máximo pode ser encontrado se encontrarmos o ponto onde a derivada é nula. Então:
Resposta
(a)
(b)
(c)