UNICAMP – Física 1 – 2020 – P1 – Discursiva
Q – Um bloco de inércia se desloca com velocidade e atinge uma mola que esta presa a um segundo bloco de inércia que tem velocidade . A inércia da mola é desprezível em relação às outras inércias. A mola é comprimida e depois volta a sua posição normal sem dissipar energia.
Quais são as velocidades finais dos dois blocos?
Que fração da energia cinética inicial o bloco perde?
No caso particular onde , faça o gráfico da fração versus e comente as situações para , e .
Passo 1
Vem comigo que a gente resolve essa juntos!
Para esse problema teremos que usar a conservação de momento e de energia cinética.
O enunciado diz que a mola não dissipa energia, e como ela é comprida e depois volta a posição normal podemos desconsiderar a energia potencial da mola.
Passo 2
Item .
Da conservação do momento temos que:
Da conservação de energia temos:
Passo 3
Dividindo o que encontramos da conservação de energia pelo o que encontramos da conservação de momento, temos:
Passo 4
Agora vamos pegar o que encontramos no final do passo anterior e isolar , assim temos:
Substituindo no que encontramos na conservação do momento, temos:
Fazendo o mesmo raciocínio para acharmos , temos:
Passo 5
Item .
Agora vamos ver a fração de energia que o bloco perde, essa fração é dada por:
Onde é a variação da energia cinética do bloco , então temos que:
Assim temos que:
Com isso temos que:
Substituindo com a expressão que temos para , temos:
Passo 6
Item .
Agora para o caso em que , temos que:
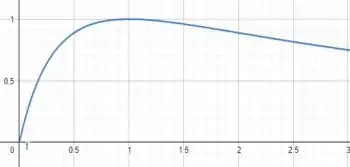
Assim o gráfico de versus fica da seguinte forma:
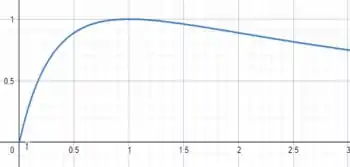
Olhando o gráfico vemos que para , onde temos , o bloco perde toda a energia cinética.
Então o lado esquerdo do gráfico do ponto temos que com isso o bloco perde velocidade, mas não inverte o sentido, mas para o lado direito do gráfico do ponto temos que , assim o bloco perde velocidade e inverte sua velocidade.
Resposta
