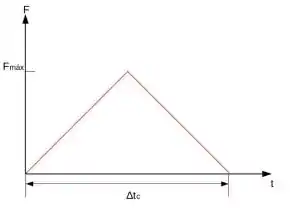
Uma bola de tênis, com massa desconhecida, é lançada com velocidade =37,5 i [m/s] e colide, elásticamente, contra uma parede, a força da colisão na parede, dada pelo gráfico ao lado, produz um impulso sobre a bola J= 4,5 Kg.m/s (-i). A força máxima na colisão é =2250 N e ocorre em Δtc/2. Determine:
- O vetor velocidade da bola após perder o contato com a parede.
- A massa da bola.
- O tempo da colisão.
- Variação da energia cinética do sistema bola-parede entre os instantes imediatamente antes da colisão e imediatamente depois de deixar o contato com a parede.
- Variação do momento linear da bola entre os instantes imediatamente antes da colisão e imediatamente depois de deixar o contato com a parede.
Passo 1
Vamo começar então entendendo a situação, beleza?
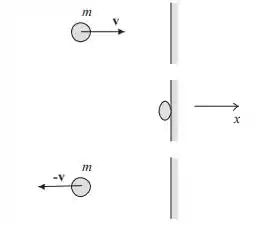
Temos algo dessa forma! E como é uma colisão elástica, a gente sabe que a Energia Cinética se conserva devido a velocidade ser constante, apenas muda seu sentido! Então nossa letra é exatamente o mesmo vetor velocidade inicial, mas com o sinal contrário, sacou?
Passo 2
Pra gente calcular a massa da bola é só a gente lembrarlá do teorema do Impulso – Quantidade de Movimento, que nos diz que:
Como vimos na letra a, , então temos:
A questão nos deu a velocidade inicial e o impulso, então é só substituir! Show!
Passo 3
E agora pra saber o tempo de colisão é só a gente lembrar que:
Então:
Como a colisão acontece na metade desse valor, temos:
Passo 4
Como a nossa colisão é elástica, nossa variação de Energia Cinética é 0, lembra?? Se quiser, podemos até calcular pra provar isso:
Show!
Passo 5
Como a gente viu na letra b:
Então a variação de momento será exatamente 4,5J! Fechamosss!
Resposta
- -37,5m/s(i)
- 60g
- 0,001s
- 0
- 4,5J