A partícula , de massa , desliza para a direita ao longo do eixo em um piso sem atrito com uma velocidade escalar de . Quando chega ao ponto no instante , ela sofre uma colisão elástica unidimensional com a partícula de massa , que estava inicialmente em repouso, conforme a figura ao lado.

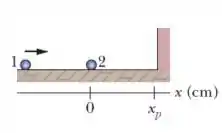
Após a colisão, a partícula se chocará com uma parede localizada no ponto (ver figura acima). Considerando essa colisão elástica, e a massa da parede muito maior que a da partícula , qual a velocidade da partícula após essa colisão dela com a parede?

Após colidir com a parede, a partícula irá colidir novamente com a partícula ? Se sim, calcule em que posição e em que instante essa nova colisão irá ocorrer, e calcule também as novas velocidades finais de e após essa colisão (considerando colisão elástica). Se não, justifique.

Começando pelo item , precisamos calcular a velocidade da partícula após a colisão.

Mas, tem um bizu muito importante aqui: como a partícula está colidindo elasticamente com uma parede (que possui massa muuuuito maior que , para que haja conservação da energia mecânica na colisão elástica, a partícula permanecerá com a mesma velocidade em módulo, porém com sentido contrário.

Assim, podemos escrever que após a colisão com a parede, vale:

Excelente!

Agora precisamos verificar se as partículas irão colidir novamente.

Como após colidir com a parede, a partícula movimenta-se para a esquerda com velocidade de e a partícula desde a primeira colisão se movimenta para a esquerda com uma velocidade de . Temos que:

Como a velocidade relativa é maior do que zero, e não foi imposto limite de tamanho à esquerda para a superfície horizontal, podemos afirmar que as partículas irão colidir novamente.

Vamos então calcular a posição e o instante em que deverá ocorrer essa colisão.

Para isso precisamos determinar a distância entre as partículas no instante em que colide com a parede.

Sabemos que:

Já para , sabemos que em tínhamos .

Se está agora em , é porque passou um intervalo de tempo dado por:

Nesse tempo, a nova posição da partícula é dada por:

Assim, a distância entre e quando se choca com a parede é dada por:

Portanto, lembrando que a velocidade relativa entre as partículas é dada por , temos que o intervalo de tempo em que ocorrerá a segunda colisão vale:

Logo:

Esse é o instante em que ocorrerá a nova colisão. A posição pode ser dada por:

Excelente!

Pra finalizar a questão, precisamos descobrir as novas velocidades das partículas e após a colisão. A ideia aqui é usarmos novamente as equações da conservação da quantidade de movimento e da energia mecânica.

Daí, pela conservação da quantidade de movimento:

Os sinais vêm da suposição que todas as partículas estarão se movendo para a esquerda após a colisão.

Já pela conservação da energia mecânica, teremos:

Assim:

Da equação da quantidade de movimento, temos:

Substituindo na equação da energia mecânica, temos:

Multiplicando por em ambos os lados:

Logo, por bháskara:

A primeira solução não tem sentido físico, pois resultaria em uma (ambas apontando para a esquerda). Assim, a segunda solução matemática é a correta.

Logo:

Prontinho gente, com isso encerramos essa questão!

Muito obrigado pela atenção e até a próxima 😊