UFABC – Fenômenos Mecânicos – Lista 5 – Questão 08
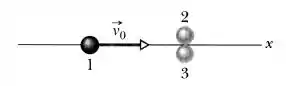
As três bolas da figura são idênticas. As bolas 2 e 3 estão se tocando e alinhadas perpendicularmente à trajetória da bola 1. A velocidade da bola 1 tem módulo e está dirigida para o ponto de contato das bolas 2 e 3. Após a colisão, quais são
(a) o módulo e
(b) a orientação da velocidade da bola 2,
(c) o módulo e
(d) a orientação da velocidade da bola 3 e
(e) o módulo e
(f) a orientação da velocidade da bola 1?
(Sugestão: sem atrito, cada impulso está dirigido ao longo da reta que liga os centros das bolas envolvidas na colisão e é perpendicular às superfícies que se tocam.)
Passo 1
Oi pessoal, tudo bem? Essa questão parece complicada, mas vou fazer passo a passo contigo!
O problema nos diz que uma bolinha de bilhar bate em outras duas conforme mostra a figura. Ele nos dá a velocidade inicial da bolinha 1 e nos diz que essa bolinha está dirigida para o centro das outras duas.
Então, que tal dar uma olhada na figura que ilustra o problema:
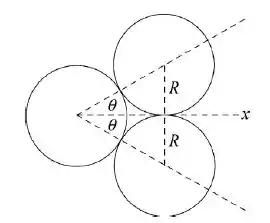
A bola incidente exerce um impulso de mesmo módulo sobre as outras duas bolas, ao longo da reta que liga o centro da bola incidente ao centro da bola que sofre o choque.
As bolas que sofrem o choque se afastam ao longo dessas retas, enquanto a bola incidente continua a se mover ao longo do eixo . Analisando a figura, observamos que os ângulos assinalados na figura valem (já que temos um triângulo equilátero quando ligamos os centros das bolas, aí o ângulo interno é e assim )
O momento linear total é conservado. Então a ideia aqui é equacionar as componentes do momento linear total em x e em y, e igualar o momento inicial com o final. E usar também a conservação de energia!
Mas relaxa, vou fazer junto com você!
Passo 2
Como falei ali no passo anterior, a componente do momento total do sistema de três bolas é conservada.
O momento inicial é apenas , já que as outras duas bolas estão em repouso. Depois da colisão elas se movem ao longo das direções indicadas aqui:
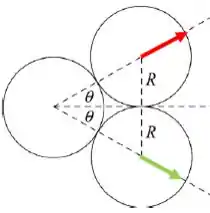
Então as componentes horizontais dos momentos das bolas 2 e 3 são iguais e valem . Já a bola 1 segue na direção horizontal, então seu momento final é .
O momento total deve ser igual ao inicial, assim temos que:
Beleza? Vamos guardar essa equação!
Agora vamos olhar para a energia cinética!
Passo 3
Bom pessoal, como a energia cinética total é conservada, temos que:
Tranquilo?
Temos duas equações e duas incógnitas (lembra que foi dado)! Então a gora partiu resolver esse sistema!
Passo 4
Letra (a): Agora vamos juntar tudo isso!
A equação que pedi para você guardar é essa aqui
E elevando ao quadrado temos o seguinte:
Certo?
Agora vamos resgatar a equação que envolve as velocidades que achamos a partir da conservação de energia cinética:
Dividindo tudo por :
Substituindo na segunda equação e explicitando , obtemos
Agora é só álgebra:
Dividindo tudo por e isolando ele do lado esquerdo:
Por fim isolando e substituindo os valores , :
De acordo com o cálculo acima, o módulo da velocidade da bola 2 é .
Passo 5
Letra (b): Bom pessoal, como percebemos no item 2, a velocidade da bola 2 faz um ângulo de no sentido anti-horário com o semieixo x positivo, vou colar aqui o desenho de novo:
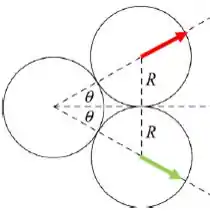
Tranquilo?
Passo 6
Letra (c): no nosso sistema, consideramos que a velocidade das bolas 2 e 3 tem módulos iguais, pois elas têm massas iguais. Sendo assim, velocidade da bola 3, é igual da bola 2 e vale .
Mas e sua orientação?
Passo 7
Letra (d): Bom pessoal, usando um raciocínio análogo aos dos itens anteriores, sabemos que a velocidade da bola 3 faz um ângulo de no sentido horário com o semieixo positivo. Essa velocidade deve ser orientada para baixo, para haver conservação de momento! Beleza?
Vamos calcular agora o módulo e orientação da bola 1?
Bora lá! Estamos quase no fim!
Passo 8
Letra (e): Então, resgatando a equação para lá do passo 4, podemos calcular :
Assim, o módulo da velocidade da bola 1 é . E sua orientação?
Passo 9
Letra (f): Reparem que o sinal negativo mostra que, após o choque, a bola 1 se move no sentido negativo do eixo . Então o ângulo é .
Beleza? Espero ter ajudado!