Dois corpos sofrem uma colisão elástica unidimensional ao longo de um eixo . A figura mostra a posição dos corpos e do centro de massa em função do tempo quando estes entram na região . Pode-se dizer que:
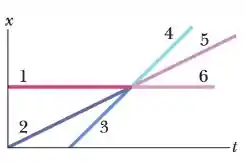
(a) A massa do corpo que estava se movendo mais depressa antes da colisão é igual à do outro corpo.
(b) As retas e representam os movimentos dos corpos depois da colisão.
(c) Os dois corpos estavam se movendo antes da colisão.
(d) A reta representa o movimento do centro de massa antes da colisão.
(e) A massa do corpo que estava se movendo mais depressa antes da colisão é maior que a do outro corpo.
Passo 1
Primeiro vamos entender esse gráfico.
Temos um gráfico da posição pelo tempo e nele estão representadas as posições da partícula , da partícula e do Centro de Massa .
A posição do Centro de Massa é nada mais do que uma média entre as posições das duas partículas, ou seja, o CM sempre vai estar sempre entre as duas partículas...
Além disso, quando temos uma reta com uma certa inclinação nesse gráfico, isso significa que a posição está variando e portanto a partícula anda com uma certa velocidade, enquanto uma reta horizontal indica uma velocidade nula.
Se considerarmos um instante antes da colisão:
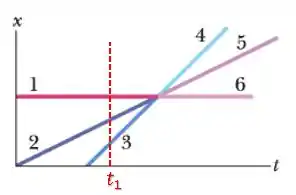
Podemos ver que a reta representa a posição do CM, pois é a posição que está entre as duas partículas:
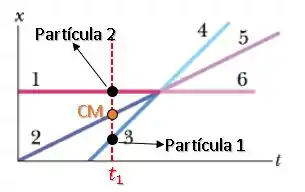
Além disso, como a reta da Partícula é horizontal, sua posição é constante, ou seja, ela está parada antes da colisão:
Enquanto a Partícula 1 anda com uma certa velocidade .
Depois disso, acontece a colisão nesse ponto aqui:
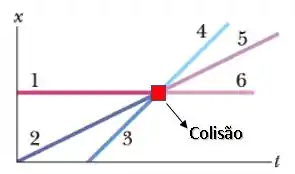
Após a colisão, há uma mudança nas velocidades de cada partícula...
Olhando para o instante , após a colisão:
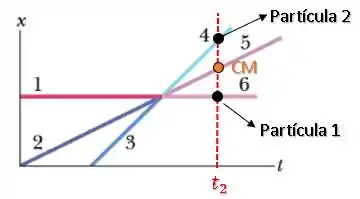
A Partícula 1 passa a ficar parada, já que a reta da sua posição é horizontal.
Enquanto a Partícula 2 passa a andar com uma velocidade , já que a reta da sua posição agora esta inclinada.
Apenas com essa análise, já eliminamos as letras (b), (c) e (d).
Agora, vamos tentar aplicar as equações de uma colisão para esse problema e tirar alguma conclusão sobre as massas.
Passo 2
Como o sistema é isolado, temos a conservação do momento linear:
Inicialmente, apenas a partícula 1 se move, então o momento linear inicial é:
Já após a colisão, apenas a partícula 2 se move, então o momento linear final é:
Aplicando na conservação, ficamos com:
Passo 3
A outra relação que podemos tirar é que a colisão foi elástica.
Isso significa que a energia cinética do sistema se conserva:
Considerando novamento apenas a partícula 1 se movimentando no início e apenas a partícula 2 se movimentando após, temos:
Passo 4
Então, temos um sistema assim:
Da primeira equação, podemos isolar o :
Substituindo isso na segunda, ficamos com:
Cortando dos dois lados:
Ou seja, considerando que o momento linear se conservou, a única maneira de a energia cinética também se conservar é caso as duas massas sejam iguais.
Assim, ficamos com a letra (a).
Resposta
Letra (a)