Um disco de massa colide com um bloco de massa na ausência de forças externas. Após a colisão, o bloco adquire momento linear na direção e a componente do momento linear do disco é conservada (veja a figura abaixo).

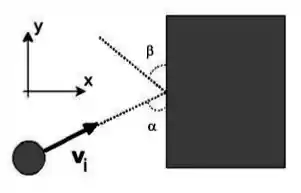
Admitindo que a colisão é elástica, se , a componente da velocidade final do disco pode ser escrita em termos da componente da sua velocidade inicial como:

nenhuma das outras alternativas.

A conservação da energia cinética nos dá que

Como o bloco não adquire velocidade no eixo , podemos dizer que energia cinética do eixo se manteve assim, como a energia cinética do eixo

Temos uma relação entre a velocidade dos blocos e a velocidade inicial e final do disco

Podemos substituir essa relação na equação que encontramos no passo

Mas, ainda vimos que é