Considere dois blocos inicialmente parados nas extremidades de uma rampa sem atrito como ilustrado na figura abaixo. O bloco vermelho tem massa e energia , enquanto o bloco azul tem massa e energia . Os blocos são soltos e ao alcançarem a superfície plana da rampa toda a energia está em forma de energia cinética.
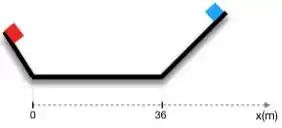
Calcule a posição onde os blocos sofrerão uma colisão.
Considere uma colisão perfeitamente elástica entre os blocos. Calcule as velocidades finais de cada bloco e o coeficiente de restituição da colisão.
Esboce, num único gráfico, a energia cinética de cada bloco e a energia cinética do sistema em termos da posição na parte plana da rampa.
Passo 1
Vem comigo que a gente detona com essa questão!
O lance desse problema é usar a conservação de energia dada por:
Para encontrar a velocidade de cada bloco na parte plana antes da colisão.
Na situação da colisão como temo uma colisão perfeitamente elástica, o momento e a energia são conservados.
Vamos então as contas.
Passo 2
Vamos começar com o item .
Para saber a posição que eles vão se bater, precisamos saber a velocidade deles na parte, plana. Vamos usar a conservação de energia para cada um deles.
Para os dois blocos, como eles partem do repouso eles só tem energia potencial (que o enunciado nos deu), no final da rampa eles só vão ter energia cinética.
Vamos começar com o bloco vermelho, temos:
Substituindo os valores que conhecemos, temos:
Agora para o bloco azul, temos:
Substituindo os valores que conhecemos, temos:
Passo 3
Sabemos agora a velocidade do bloco vermelho e do bloco azul, o que podemos fazer agora é calcular quanto tempo leva para eles colidirem, vamos usar a seguinte equação:
Nesse caso teremos que é quando eles colidem, e já que eles estão se aproximando, assim:
Eles levaram para colidir, podemos achar isso e ver quanto o bloco vermelho andou até isso acontecer, vamos usar ele porque a base da rampa nele é que começa o ponto zero, assim:
Então eles colidem em .
Passo 4
Agora para o item .
Temos que calcular a velocidade de cada bloco depois da colisão.
Para isso vamos usar a conservação de momento e a conservação de energia, que com isso conseguimos saber a velocidade de cada bloco depois da colisão e sabendo isso a gente pode calcular a energia cinética de cada um.
Temos o seguinte para a conservação do momento:
Para a conservação da energia temos:
Dividindo o que encontramos na conservação da energia por o que encontramos na conservação de momento, temos:
Passo 5
Agora substituindo os valores de e no que encontramos, temos:
Substituindo isso na equação que chegamos na conservação de momento, temos:
Substituindo os valores conhecidos, temos:
Então temos que:
Então a velocidade dos blocos se manteve a mesma.
O coeficiente de restituição de colisão é dado por:
O que faz sentido já que a colisão é perfeitamente elástica.
Passo 6
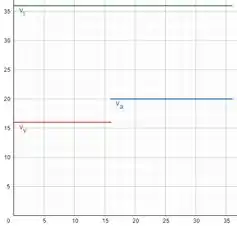
Agora para o item temos que desenhar o gráfico da energia cinética de cada bloco e do sistema.
A energia cinética antes da colisão dos blocos é a mesma que o enunciado forneceu, já que toda a energia potencial virou energia cinética, como as velocidades se mantem as mesmas depois da colisão a energia cinética de cada bloco também não vai mudar.
O gráfico dessa energia cinética fica da seguinte forma:
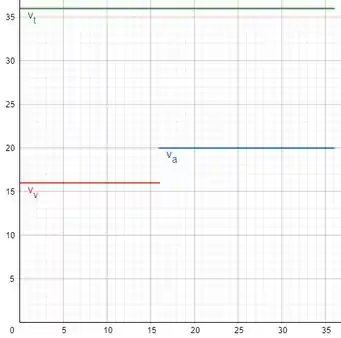
Resposta