Duas bolas e , de massas e diferentes, colidem elasticamente. Inicialmente a bola tem velocidade , onde é uma constante positiva, e a bola está em repouso. Após a colisão a bola passa a se mover com velocidade , na direção perpendicular à direção do movimento inicial. Considere o plano da colisão como sendo horizontal e despreze as forças de atrito.
(a) Faça um esboço dos vetores velocidades das bolas e após a colisão, indicando o sistema de coordenadas e os ângulos envolvidos.
(b) Escreva o sistema de equações que a partir do qual é possível determinar a direção e a magnitude da velocidade da bola após a colisão. Justifique cada uma destas equações.
(c) Determine o ângulo entre e a direção .
(d) Determine o vetor e seu módulo em função de .
Passo 1
Inicialmente a bola anda na horizontal e a bola está parada:
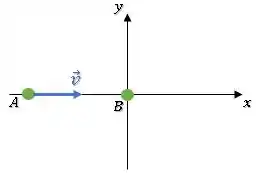
Na letra (a), queremos o esboço após a colisão.
Após a colisão, a bola sai com uma velocidade na vertical para cima ().
Vamos ver mais a frente que o momento linear se conserva e por isso a bola deve ter uma componente de velocidade na vertical para baixo (contrapondo ) e também uma componente de velocidade na horizontal (mantendo o momento linear inicial):
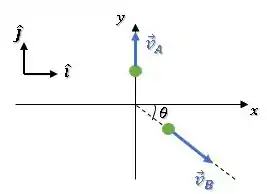
Passo 2
Na letra (b), queremos as equações que precisamos para descobrir .
Vamos trabalhar com duas ideias!
A primeira delas é o seguinte, como o plano é horizontal (força peso e normal se anulam) e não há força de atrito, temos que o sistema está livre da ação de forças externas.
Assim, podemos dizer que o momento linear do sistema se conserva:
Podemos abrir esses vetores nas componentes em e em e escrever que os momentos lineares se conservam nas duas direções:
Já a segunda ideia vem de que a colisão é elástica.
Em uma colisão é elástica, a energia cinética do sistema se conserva, portanto:
Passo 3
Agora vamos escrever cada uma daquelas equações.
Vamos começar com o momento linear.
Na horizontal:
Inicialmente, temos:
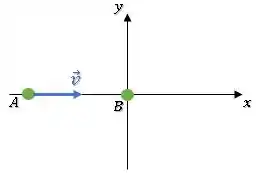
Como o módulo da velocidade de é , temos:
Para escrever os momentos em cada direção, vamos decompor a velocidade de após a colisão:
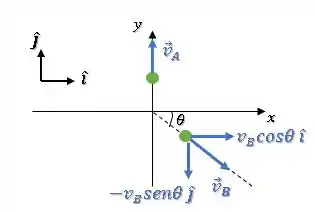
Já o momento linear final na horizontal será:
Conservando o momento linear na horizontal, temos:
Na vertical:
Inicialmente, o momento linear em é nulo:
Já após a colisão, temos:
Conservando o momento linear na vertical, temos:
Passo 4
Agora, vamos usar a conservação da energia cinética:
A energia cinética leva em consideração apenas o módulo da velocidade e não a sua direção.
Inicialmente, temos apenas a energia cinética da bola :
Já no final, temos tanto a energia cinética da bola quanto a da :
Conservando a energia cinética, ficamos com:
Pronto, conseguimos nossa terceira equação e ficamos com um sistema assim:
Passo 5
Na letra (c), queremos achar o ângulo .
Para isso, vamos trabalhar com o nosso sisteminha.
Como, inicialmente só estamos interessados no ângulo . Um bom macete para relacionar uma expressão com seno e a outra com cosseno é dividindo uma pela outra.
Então, dividindo a segunda equação pela primeira :
Podemos cortar todas as massas e velocidades:
Ou seja, será o arco cuja tangente vale :
Passo 6
Na letra (d), queremos tanto o vetor velocidade da bola , quanto seu módulo.
Voltando o nosso sisteminha:
Como queremos achar , vamos usar qualquer outro parâmetro menos ele para substituir de uma equação para outra.
Podemos por exemplo isolar na primeira e substituir na terceira :
Substituindo isso na terceira equação, temos:
Cortando :
Cortando um dos termos de e :
Porém, só queremos em função de . Então, temos que dar um jeito de tirar esse daí.
Vamos tentar usar a relação que achamos para :
Passo 7
Para encontrar esse , vamos usar a relação fundamental:
Dividindo tudo por , conseguimos relacionar a tangente com o cosseno:
Substituindo o valor que achamos para tangente, temos:
Vamos aproveitar essa trigonometria para achar o seno também, pois vamos precisar disso na hora de escrever o vetor :
Passo 8
Substituindo o valor de cosseno na expressão de , ficamos com:
Achamos o módulo, agora só falta escrever o vetor :

Resposta
(a)
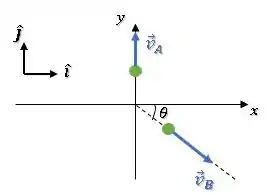
(b)
(c)
(d)