UFSCAR – Sem Campus – Física 1 – AV3 –2021.2 – Prof. Raphael Santarelli – Questão 4b
Uma barra de comprimento e massa repousa sobre uma mesa horizontal sem atrito. Um pequeno objeto de massa movendo-se com velocidade , como mostra a figura ao lado (visão de cima), colide elasticamente com a barra a uma distância de seu centro.
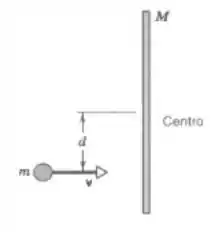
b) Qual deve ser a massa do objeto para que ele fique em repouso após a colisão? DICA: Aplique as leis de conservação enunciadas no item anterior, e considere que no final a barra irá transladar + girar em torno de um eixo que passa pelo próprio centro de massa dela.
Passo 1
Eaee!!! Belezinha? Bom... a questão nos dá um sistema de colisão de uma bolinha em uma barra e nos pede para qual deve ser a massa do objeto para que ele fique em repouso após a colisão.
Uma dica é analisarmos as forças e os torques que atuam no sistema antes e depois da colisão!
E aí? Bora lá?
Passo 2
Bom... Pela conservação de energia, temos que a energia cinética antes da colisão tem que ser igual a que vem depois da colisão :
Assim, substituindo, temos:
Passo 3
Por outro lado, pela conservação do momento linear :
Passo 4
Pela conservação do momento angular :
Passo 5
Substituindo as equações dos Passos 3 e 4 na equação do Passo 2 (sabendo que ):
Entendeu direitinho? Responde aee ;)
