Um bloco de massa está em equilíbrio preso a uma mola ideal, de constante elástica , inicialmente em sua posição relaxada, como mostra a figura. Uma bala de massa com velocidade horizontal de módulo colide com esse bloco de modo que a bala retorna após a colisão no sentido oposto com velocidade de módulo .
Considere que: a colisão é instantânea; que a mola é ideal; que a resistência do ar é desprezível; e que a gravidade tem módulo conhecido.
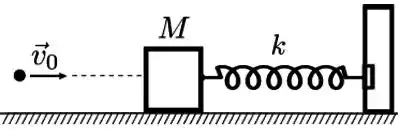
Determine, em função dos dados do problema:
A razão para que a colisão seja elástica.
Passo 1
Para a colisão ser elástica, a energia cinética deve se conservar!
Antes da colisão, o bloco está parado, então a energia cinética total do sistema bala+bloco é a energia cinética da bala
Depois da colisão, a velocidade da bala é e a do bloco é . Então a energia cinética final do sistema é
Logo, a equação de conservação da energia cinética é:
Passo 2
Bom, temos as massas as quais queremos saber a razão entre elas, mas ainda temos a velocidade do bloco como incógnita, então temos que descobri-la e faremos isso por conservação de momento linear.
Como estamos estudando uma colisão, e o enunciado ainda fez questão de enfatizar ser instantânea, vamos usar a relação que na colisão há conservação de momento linear, então
Vamos analisar o momento linear antes do impacto:
A bala tem massa e velocidade inicial de módulo , enquanto o bloco tem massa , mas está parado.
Vamos definir o sentido de (pra direita) como positivo. Então o momento linear total do sistema bala+bloco logo antes da colisão, em módulo, é:
Passo 3
Agora o momento linear depois da colisão:
Logo após a colisão, a bala volta com velocidade de módulo no sentido oposto, então sua velocidade agora é negativa. E o bloco vai ter a velocidade , que é justamente o que a gente quer achar!
Então o módulo do momento linear total do sistema logo após a colisão é:
Voltando pra equação da conservação do momento linear:
Passo 4
Agora que temos , podemos resolver a equação que achamos pela conservação de energia, basta multiplicar tudo por 2 e substituir :
Podemos dividir tudo por , aí sobra:
Então pra colisão ser elástica, devemos ter