Energia Potencial e Conservação da Energia Mecânica, Colisões
Um corpo de massa desce, a partir do repouso, uma rampa semiesférica de raio sem atrito, partindo da mesma altura do centro rampa. Ao chegar no ponto mais baixo ele colide com outro corpo de massa que se encontrava ali em repouso. Considere a colisão elástica e com . Encontre a altura que o corpo 2 sobe em função de .
Tome .
Passo 1
Vou fazer um esqueminha simples pra gente visualizar melhor:
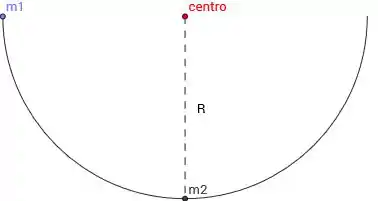
Vou dividir o estudo do movimento em 3 partes: a descida da , a colisão e a subida de , show?
Passo 2
Descida de :
Podemos começar calculando com que velocidade a massa tem logo antes de colidir com . Pra isso, podemos aplicar a conservação da energia mecânica (já que ):
sendo a energia mecânica da massa assim que ela inicia a descida e a sua energia mecânica logo antes da colisão com .
Seja a energia cinética e a energia potencial gravitacional, então
Logo,
Passo 3
A massa parte do repouso então sua velocidade inicial é nula, assim como sua energia cinética (). Além disso, sua energia potencial gravitacional inicial é , então:
Logo antes da colisão, a massa não tem energia potencial gravitacional, então , o que dá:
que é aquele resultado clássico de metade dos exercícios de Física 1 rs.
Usando isso dá
Passo 4
Colisão:
Vamos começar aplicando a conservação do momento linear total. Sendo e o momento linear do sistema logo antes e logo depois da colisão, respectivamente, temos
Passo 5
E logo antes da colisão, a massa está parada, logo o momento linear total é:
Passo 6
Logo depois da colisão, podemos definir e como as velocidades das massas e , respectivamente. Então o momento linear total é
Como isso dá
Passo 7
Ou seja, pela conservação do momento linear:
Passo 8
Beleza, agora vamos aproveitar o fato que a colisão é elástica! Isso significa que a energia cinética total é conservada:
Passo 9
Como já vimos, logo antes da colisão está no repouso, então sua energia cinética é nula ().
Então
Passo 10
Logo depois da colisão, a energia cinética é
Passo 11
Então a conservação da energia cinética ficou
Passo 12
Recapitulando, isso tudo nos deu as equações
Portanto,
Elevando tudo ao quadrado:
Passo 13
Assumimos que a massa tem uma velocidade não nula logo depois da colisão, ou seja . Assim,
Pela 1ª equação do sistema lá de cima, temos então vamos ter
Passo 14
Subida de :
Ela parte sem energia potencial gravitacional () e sua energia cinética é:
Terminando sua subida, chega no repouso na altura onde sua energia cinética é zero e sua energia potencial gravitacional é .
Passo 15
Pela conservação da energia mecânica, temos
Fazendo , vai dar
Uhul, conseguimos! :)