Um projétil de é disparado horizontalmente com velocidade em , contra um corpo de massa suspenso por um fio de de comprimento. Em um choque perfeitamente elástico e frontal, o corpo sobe até uma altura . Qual é o ângulo máximo formado pelo fio com a vertical?
Passo 1
Fala aí, pessoal!!
Temos um corpo colidindo elasticamente com outro, que está pendurado. As massas desses dois corpos são iguais, certo?
Porque .
E aí o corpo que estava pendurado, sobe. E ele pergunta qual é o ângulo que o fio faz com a vertical nesse momento.
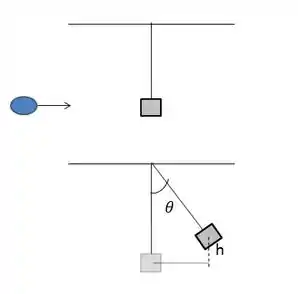
Na colisão perfeitamente elástica entre dois corpos de mesma massa há troca de velocidades. Assim a energia cinética do projétil é transferida para o corpo suspenso, e na altura máxima do corpo, estará sob a forma de energia potencial gravitacional.
Passo 2
Então:
Podemos cortar a massa, e substituindo os dados do enunciado temos:
Agora, vamos olhar para esse triângulo retângulo:
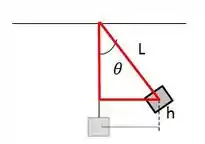
O cateto adjacente ao ângulo vale o comprimento do fio menos h. Concorda?
Calculando o cosseno desse ângulo:
Portanto,