UFSCAR, Sem Campus, Física 1, AV3 - 2021.2 - Prof° Raphael Santarelli, Questão 1a
A partícula , de massa , desliza para a direita ao longo do eixo em um piso sem atrito com uma velocidade escalar de . Quando chega ao ponto no instante , ela sofre uma colisão elástica unidimensional com a partícula de massa , que estava inicialmente em repouso, conforme a figura ao lado.
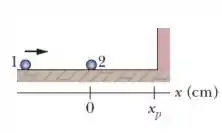
Quais as velocidades finais das partículas e após essa colisão?
Passo 1
Fala aí pessoal, tudo tranquilo?
Temos aqui uma questão de colisão elástica unidimensional. Basicamente, temos a part��cula se movendo para a direita, com uma massa e velocidade escalar de . Em , ela colide com uma partícula , de massa , que estava parada.
Nesse item precisamos determinar as velocidades de e após a colisão.
Alguma ideia de como podemos atacar o nosso problema?
Bom, a ideia principal vem de duas equações:
Conservação da quantidade de movimento antes e depois da colisão.
Assim, podemos escrever:
Conservação da energia mecânica antes e depois da colisão (pois trata-se de uma colisão elástica).
Usando essas duas equações teremos como variável apenas e . Aí é só manipular as equações e matar a questão 😊
Vem comigo!
Passo 2
Bom, vamos começar escrevendo as duas equações mencionadas no passo . Da conservação da quantidade de movimento, temos:
Para tirar o caráter vetorial dessas variáveis vamos considerar que velocidades positivas são as que apontam para a direita, e negativa são as que apontam para a esquerda.
Vamos supor também que e apontam para a direita. Assim, substituindo também os dados do enunciado nessa equação, temos:
Da conservação da energia mecânica, podemos escrever que:
Substituindo os dados do enunciado, temos:
Muito bom!
Passo 3
Agora que já escrevemos as duas equações, vamos manipulá-las para encontrar as variáveis.
De:
Substituindo na segunda equação:
Multiplicando por em ambos os lados:
Logo, por bháskara:
A primeira solução não faz sentido fisicamente, pois teríamos . Mas, sabemos que não é possível a partícula sofrer a colisão e voltar para a esquerda. Portanto, ficamos com a segunda solução:
Isso significa que após a colisão a partícula volta para a esquerda. Teremos também:
Portanto, temos:
Prontinho! Matamos mais uma questão 😊
Até a próxima pessoal!