Dentro de uma câmara, temos uma névoa formada por gotículas d'água em suspensão, com uma densidade . Considere um cubo de massa M, se deslocando horizontalmente sem atrito sobre um trilho neste ambiente, com uma velocidade inicial de módulo e direção perpendicular a uma de suas faces, de área A. Despreze a resistência com o ar e o atrito com o trilho.
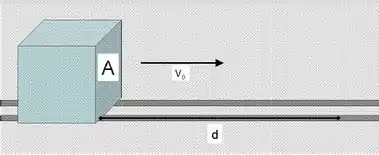
- Se o corpo absorver a água ao longo de sua passagem, apenas pela face frontal, percorrendo uma distância , qual vai ser sua velocidade final?
b) Qual a variação de energia do sistema?
c)Considere agora que no lugar de gotículas d'água, temos cristais de gelo, que sofrem colisões elásticas com a superfície do corpo. Considerando que a densidade da névoa é a mesma do caso anterior, qual a velocidade do corpo, decorrido um tempo do início do deslocamento?
Dê suas respostas em termos
Passo 1
Mano, assumo que quando vi por cima essa questão eu pensei:

Mas ao ler percebemos que temos mais uma questão “fazível” de colisões e momento linear.
Os dados fornecidos na questão foram:
Densidade da névoa:
Massa do Cubo:
Área da face:
Velocidade inicial do cubo:
Passo 2
a)
Ao se locomover, o cubo vai absorvendo a névoa e a velocidade do carro tende a diminuir pois a massa do sistema será aumentada. Pela conservação do momento linear, a gente pode dizer:
Passo 3
Ele nos disse que a densidade é , mas só lembrando, qual a fórmula da densidade?
Show! Mas esse da relação seria justamente a massa quantidade de névoa que ele vai “catar”. Essa massa de quantidade de névoa é justamento o nosso da equação acima! Assim, passando o para o outro lado a gente vai ter:
Mas pera aí, quem seria esse ?
É justamente o que a face de área consegue capturar multiplicado pela distância que ele percorre, isso nos dá um volume. ;]
Daí, podemos escrever:
Voltando para a nossa equação do momento e isolando o teremos:
Passo 4
b)
Ah, a varição de energia será apenas a cinética, o .
Substituindo pelo que achamos na letra a, vamos ter:
Passo 5
c)
Show!Como agora a névoa muda inocentemente para cristal e as colisões serão elásticas muito provavelmente os cristais e o cubo não terão a mesma velocidade, como ocorreu na letra b. Mas só em dizer que a colisão é elástica o autor já nos diz duas coisas: Momento Linear é conservado e a Energia Cinética também. Bora escrever essas relações:
Sendo respectivamente a velocidade final do cubo, velocidade adquirida pelos cristais e a massa da quantidade de cristais que já colidiram com o cubo.
Ah, a gente pode transformar esse em algo do tipo , já que a velocidade final nada mais é do que a velocidade inicial acrescentada ou reduzida de uma variação de velocidade. Reescrevendo a relação que a gente achou , teremos:
Isolando esse , vai ficar:
Passo 6
Agora fazendo a mesma coisa para energia cinética, vai ficar:
Desenvolvendo melhor, teremos que:
Opa, mas no passo anterior a gente chegou na relação que dizia um valor para . Substituindo esse valor na relação...
Daí a gente corta os e .
Passo 7
Talvez esse passo seja a maior dificuldade dessa questão, aquela bendita “sacada” que resolve tudo. Saca só!
Supondo que esses cristaisinhos sejam mega-ultra-power-minion pequenos em comparação ao cubo, a massa do cubo vai ser beeeeeem maior que a dos cristais e assim podemos aproximar a soma .
Desta forma a nossa relação vai ficar:
Passo 8
Show of Ball! Mas daí depois desse tempo todo a gente pensa: “Quem será esse ?”
Como falei lá em cima o é a massa dos cristais de gelo que o cubo vai colidindo, e como fizemos lá no Passo 3, podemos reescrever essa massa de tal forma:
O nosso problema é que pra essa letra c ele nem falou em “d”. :/
Lembrando lá da cinemática a gente sabe que e desta forma a gente pode reescrever essa equação, já que ele nos deu um .
Substituindo novamente lá na fórmula do Passo 7, vai ficar:
Passo 9
Tá lindo! Pra concluir aqui, a gente pensa: “ Ah, e se a gente considerar esses tão pequenos que possamos substituir por um diferencial?”. Vai ficar isso aqui, oh:
Aí, meu amigo é só integrar e correr pro abraço!