Um disco de massa colide com um bloco de massa na ausência de forças externas. Após a colisão, o bloco adquire momento linear na direção e a componente do momento linear do disco é conservada (veja a figura abaixo). Admitindo que a colisão é elástica, podemos afirmar que:
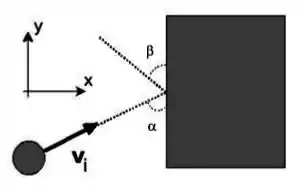
o ângulo de incidência do disco é igual ao ângulo de reflexão .
o ângulo de reflexão não depende da relação das massas do disco e do bloco.
o ângulo de reflexão é menor que o ângulo de incidência .
o ângulo de reflexão é maior que o ângulo de incidência .
o ângulo de reflexão é zero.
Passo 1
Como estamos tratando de uma colisão elástica o momento linear e a energia cinética irão se conservar.
O enunciado diz que após a colisão o bloco de massa adquire velocidade na direção e o disco mantem o mesmo momento linear na direção .
Para o momento linear em se conservar, temos que
Onde é dado por:
Como vimos que elas são iguais então chegamos que
Passo 2
Achamos uma relação entre os ângulos e as velocidade, mas ainda não sabemos nada sobre a velocidade do disco após a colisão
Para isso vamos usar o fato da energia cinética se conservar
Como é sempre maior ou igual a zero, temos que:
Se , então
Voltando nas equações que encontramos quando fizemos conservação de momento em .
Como a relação dos cosseno de um ângulo e o ângulo é inversa, quero dizer que quanto menor o ângulo maior o cosseno. (caso do ângulo estar entre )
Sendo assim, descobrimos que
Pela conservação de momento na direção , temos:
Assim, vemos que as massas e vao influenciar no anglo e nas velocidades e .
Então a alternativa correta é a que diz que . O valor de vai depender das massas.
Resposta
Alternativa