Uma haste fina e homogênea , de massa e comprimento , é livre para girar numa mesa de ar horizontal (sem atrito) em torno de um eixo vertical que passa pela extremidade . Uma bola rígida de massa é lançada com velocidade contra a extremidade enquanto a haste está em repouso. A colisão é elástica e a bola fica em repouso imediatamente após a colisão.
Dado: o momento de inércia da haste em relação ao eixo de rotação é .
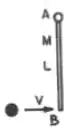
- Determine a massa da bola em termos da massa da haste.
- O momento linear do sistema bola haste se conserva na colisão? Justifique sua resposta.
Passo 2
Vamos começar com as conservações!
A força exercida pelo eixo de rotação passa pelo ponto da haste, logo o torque externo em relação a este ponto é zero e o momento angular, em relação também a este ponto, se conserva.
O enunciado diz que a colisão é elástica, logo ocorre conservação da energia cinética.
Passo 3
Sendo a velocidade angular da haste logo após a colisão, temos:
Passo 4
Calculando o sistema, chegamos em:
Passo 5
Como foi dada na questão a equação do momento de inércia, vamos substituir na equação acima.
Passo 6
Para que haja conservação do momento linear é necessário que não tenham forças externas atuando no sistema. Como vimos no passo 1, existe uma força exercida pelo eixo de rotação, sendo ela externa ao sistema. Logo, o momento linear não se conserva.
Resposta
- O momento linear não se conserva devido a presença de uma força externa exercida no eixo de rotação do ponto .