Um bloco de massa deslizando sobre uma mesa horizontal, com coeficiente de atrito cinético colide com uma mola de massa desprezível, de constante de mola inicialmente na posição relaxada. O bloco atinge a mola com velocidade de .
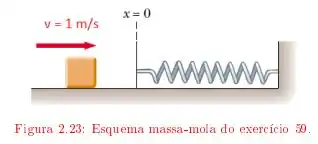
Qual é a deformação máxima da mola?
Passo 1
Fala aí galera, tudo beleza?
Aqui temos um bloco que atinge uma mola , inicialmente relaxada, com velocidade de . Na superfície horizontal em que a mola se encontra, tem um atrito de .
Queremos determinar a deformação máxima da mola.
Alguma ideia de como podemos fazer isso já que agora temos o atrito envolvido também?

Então, podemos usar o princípio do trabalho das forças não conservativas. Basicamente, o somatório do trabalho das forças não-conservativas é igual à variação de energia mecânica do sistema:
Show de bola! Sabendo disso vamos descer a mão na questão!
Vem comigo 😊
Passo 2
Bom, a única força não-conservativa que atua no nosso sistema é a força de atrito. Assim, vamos escrever uma expressão para o trabalho realizado por essa força.
Como o bloco está em equilíbrio na vertical:
Assim:
Beleza! Como essa força é constante, considerando um deslocamento até o bloco atingir a deformação máxima da mola, temos:
Tranquilo?
Já sobre a variação da energia mecânica, basta lembrarmos que ela é composta por energia cinética e potencial gravitacional. Daí:
Excelente!
Passo 3
Agora vamos juntar os dois resultados que encontramos:
Como no ponto de deformação máxima a velocidade do bloco deve ser nula:
Logo:
Assim:
Substituindo os valores dados pelo enunciado:
Temos:
Dividindo tudo por temos:
Usando Bháskara:
Como a deformação máxima precisa ser positiva, vem:
Portanto:
O que é equivalente a:
Prontinho! Obrigado pela atenção pessoal 😉