Uma bola de massa , com velocidade de que faz um ângulo de com a horizontal, atinge o centro de uma placa, também de massa , que se encontra inicialmente em repouso. Durante a colisão não há atrito e, devido à colisão, podemos considerar que a placa se move apenas verticalmente. Considerando esta colisão elástica, determine:

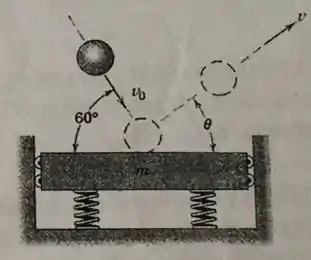
Que grandezas são conservadas nesta colisão. Justifique.

A direção e sentido dos vetores impulso atuando sobre a placa e sobre a bola.

O vetor velocidade final de ambas as massas, bola e placa, logo após o impacto.

O vetor força média que atuou na bola sabendo que o tempo da colisão foi de .

Para determinar o vetor impulso, vamos relembrar sua definição:

No caso da placa, como não há movimento no eixo nem antes nem depois da colisão temos que o impulso é zero.

Já no eixo , pela equação de momento temos

Como o momento inicial da placa é zero, pois ela estava em repouso, descobrimos que haverá impulso na direção

Agora só precisamos descobrir o sentido desse vetor. Para isso vamos abrir a equação de momento

Onde é a velocidade da placa depois da colisão, olhando a imagem vemos que a bola vai colidir com a placa e empurrá-la para baixo, assim o único sentido possível para o movimento da placa é para baixo (sentido negativo do eixo ).

Sendo assim definimos o sentido da velocidade da placa que será negativa, implicando que o impulso em será no sentido negativo também.

Assim o vetor impulso na placa é dado por

Agora vamos estudar o caso da bola,

Como no item dissemos que o momento linear se conserva, devido a isso sabemos que o impulso resultante no sistema deve ser zero.

O nosso sistema é composto por bola e placa, terminamos de dizer a direção e sentido do impulso na placa, para que a resultante do impulso no sistema seja zero, temos que o impulso na bola é na mesma direção e módulo do impulso na placa, porém com o sentido oposto.

O impulso na bola pode ser dado por

Para descobrirmos a velocidade final da bola, vamos aplicar conservação de momento em cada eixo do sistema.

Começando pelo eixo , pois apenas a bola consegue se movimentar nesse eixo.

Sendo assim temos que

Cortando a massa e isolando , chegamos na primeira equação

Agora, vamos analisar o eixo , onde por conservação de momento temos

No momento antes da colisão só a bola se movimentava e depois da colisão a bola continua a se movimentar, mas a placa começa a se movimentar também, então podemos reescrever a fórmula acima

Como já vimos é negativa, e podemos cortar a massa, chegamos na nossa segunda equação

Podemos agora substituir a primeira equação na segunda e obtemos

Lembrando que seno dividido por cosseno é tangente e isolando , chegamos na nossa terceira equação

Precisamos de mais uma equação para resolver o problema, já usamos conservação de momento linear, então agora vamos usar o fato que a energia cinética também se conserva.

Então vamos ter

Cortando tudo que se repete nos três termos da equação chegamos na nossa quarta equação

Agora, substituindo a primeira e a terceira equação na quarta temos

Precisamos resolver essa equação agora, podemos cortar

Tirando o do denominador e abrindo a tangente em seno e cosseno

Lembrando da relação fundamental, onde

Assim, chegamos na equação

Temos a solução onde , e a solução onde

Assim, a outra solução é

Essa solução não serve para gente, pois iria violar uma das conservações, basta substituir nas fórmulas para conferir.

Vamos então usar a solução , assim substituindo na primeira equação temos que a velocidade da bola depois da colisão é

Agora, para achar a velocidade da placa depois da colisão é só substituir na equação

Para calcularmos a força média aplicada na bola, vamos usar a fórmula

No “passo 2” vimos que o impulso aplicado na bola é igual

Assim,

Substituindo o valor de , e