UFES, 2018.1, Lista 3, Q15b
15b) Para a função definida por:
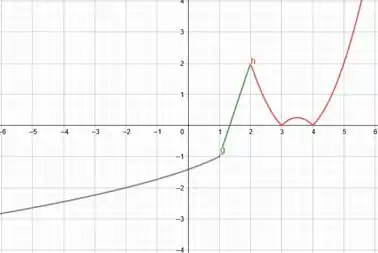
Esboce o gráfico de .
Passo 1
Bom, pelo resultado encontrado no item a), já temos e . Assim, vamos reescrever a lei da função antes de montar o gráfico, beleza?
Passo 2
Agora, como já possuímos a lei da função, bora montar esse gráfico:
A primeira parte que vamos desenhar é justamente no intervalo .
Nesse trecho, . É uma função meio ruim de desenhar, mas é só fazer uma curva um pouco suave até o ponto da extremidade, em que o valor de é dado por:
(Lembrando que a igualdade só acontece porque é contínua.)
Beleza, vamos pra segunda parte, no intervalo .
Nesse pedaço segue a equação de uma reta, então pra desenhá-la é só ligarmos os pontos das suas extremidades, ou seja, e .
Como já vimos, e . Perfeito!
Agora vamos pra última parte do gráfico, que será no intervalo .
Aqui, temos uma equação modular do 2°grau, isso significa que vamos ter uma parábola rebatida onde ela tiver valores negativos. O formato da função vai lembrar uma carinha triste onde ☹
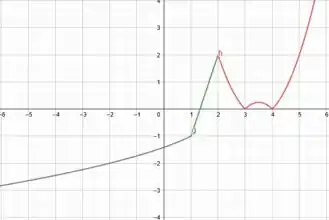
Uma forma legal de conferir se acertamos os cálculos de e é ver se, ao desenharmos o gráfico, a função realmente ficou contínua. E a nossa ficou! 😊
Resposta
