Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Equação modular

Ver Teoria
Exercício 171234567891011121314151618192021222324252627282930313233343536373839

Enunciado

Escreva as seguintes expressões sem utilizar sinais do valor absoluto, separando em dois ou mais casos quando for necessário.

x - 1 - 2 - x

Passo 1

Precisamos fazer os dos módulos, primeiro vamos pegar x - 1

x - 1 = x - 1 , x - 1 ≥ 0 - x - 1 , x - 1 < 0

Resolvendo aquela inequação, vamos ter

x - 1 ≥ 0

x ≥ 1

E

x - 1 < 0

x < 1

Resultando em

x - 1 = x - 1 , x ≥ 1 - x - 1 , x < 1

x - 1 = x - 1 , x ≥ 1 - x + 1 , x < 1

Passo 2

Vamos para o segundo módulo 2 - x

2 - x = 2 - x , 2 - x ≥ 0 - 2 - x , 2 - x < 0

Resolvendo aquela inequação, vamos ter

2 - x ≥ 0

x ≤ 2

E

2 - x < 0

x > 2

Resultando em

2 - x = 2 - x , x ≤ 2 - 2 - x , x > 2

E vamos ter

2 - x = 2 - x , x ≤ 2 - 2 + x , x > 2

Passo 3

Vamos agora juntar todos esses módulos

Temos que olhar os intervalos primeiro, para entendermos como vai ficar

x ≥ 1 x < 1       e       x ≤ 2 x > 2

Então, no fundo temos

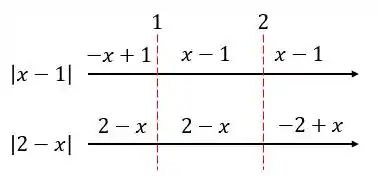
Fazendo a subtração, vamos ter

x - 1 - 2 - x = x - 1 - - 2 + x , x ≥ 2 x - 1 - 2 - x , 1 ≤ x < 2 - x + 1 - 2 - x , x < 1

Vai ficar

x - 1 - 2 - x = x - 1 - - 2 + x , x ≥ 2 x - 1 - 2 - x , 1 ≤ x < 2 - x + 1 - 2 - x , x < 1

x - 1 - 2 - x = x - 1 + 2 - x , x ≥ 2 x - 1 - 2 + x , 1 ≤ x < 2 - x + 1 - 2 + x , x < 1

x - 1 - 2 - x = 1 , x ≥ 2 2 x - 3 , 1 ≤ x < 2 - 1 , x < 1

Resposta

x - 1 - 2 - x = 1 , x ≥ 2 2 x - 3 , 1 ≤ x < 2 - 1 , x < 1

Exercícios de Livros Relacionados

Resolva as equações.|2 x + 3| = 0
Prove:|x + y| = |x| + |y| harr x y = 0
Resolva as equações.|x + 1| = 3
5 - Elimine o módulo.d) |x| + |x - 1| + |x - 2|
Resolva as equações.|x + 1| = 3