Resolva em as seguintes equações
Passo 1
Precisamos fazer os dos módulos, primeiro vamos pegar
Resolvendo aquela inequação, vamos ter
E
Resultando em
Estamos deixando os parênteses para facilitar o produto lá na frente.
Passo 2
Vamos para o segundo módulo
Resolvendo aquela inequação, vamos ter
E
Resultando em
Estamos deixando os parênteses para facilitar o produto lá na frente.
Passo 3
Vamos agora juntar todos esses módulos
Temos que olhar os intervalos primeiro, para entendermos como vai ficar
Então, no fundo temos
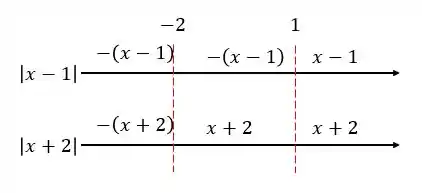
Fazendo o produto, vamos ter
Vamos ter casos para resolver, isso porque a primeira e última equações serão iguais.
Passo 4
Com ou
Resolvendo, vamos ter
E
Repara que vai ser maior que e vai ser menor que , isso porque vai ser maior que , afinal ela é maior que .
Se colocássemos nas raízes, iriamos achar e
Essas suas são valores bem próximos do real, então eles estão no nosso intervalo.
Passo
Vamos para o segundo intervalo
Assim, passando aquele para a direita, vamos ter
Resolvendo, vamos ter
Opa, temos a raiz de um número negativo. Então não temos solução real.
AS nossas únicas soluções são aqueles E que achamos no outro passo.