Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Equação modular

Ver Teoria
Exercício 241234567891011121314151617181920212223252627282930313233343536373839

Enunciado

Resolva em R as seguintes equações

x + 3 - 2 - x = 4

Passo 1

Precisamos fazer os dos módulos, primeiro vamos pegar x + 3

x + 3 = x + 3 , x + 3 ≥ 0 - x + 3 , x + 3 < 0

Resolvendo aquela inequação, vamos ter

x + 3 ≥ 0

x ≥ - 3

E

x + 3 < 0

x < - 3

Resultando em

x + 3 = x + 3 , x ≥ + 3 - x - 3 , x < - 3

Passo 2

Vamos para o segundo módulo 2 - x

2 - x = 2 - x , 2 - x ≥ 0 - 2 - x , 2 - x < 0

Resolvendo aquela inequação, vamos ter

2 - x ≥ 0

x ≤ 2

E

2 - x < 0

x > 2

Resultando em

2 - x = 2 - x , x ≤ 2 - 2 - x , x > 2

E vamos ter

2 - x = 2 - x , x ≤ 2 - 2 + x , x > 2

Passo 3

Vamos agora juntar todos esses módulos

Temos que olhar os intervalos primeiro, para entendermos como vai ficar

x ≥ - 3 x < 3       e       x ≤ 2 x > 2

Então, no fundo temos

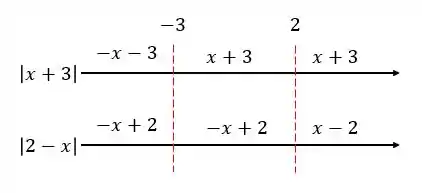
Fazendo a subtração, vamos ter

x + 3 - 2 - x = x + 3 - - 2 + x , x ≥ 2 x + 3 - 2 - x , - 3 ≤ x < 2 - x - 3 - 2 - x , x < - 3

Vai ficar

x + 3 - 2 - x = x + 3 - x + 2 , x ≥ 2 x + 3 - 2 + x , - 3 ≤ x < 2 - x - 3 - 2 + x , x < - 3

x + 3 - 2 - x = 5 , x ≥ 2 2 x + 1 , - 3 ≤ x < 2 - 5 , x < - 3

Passo 4

Queremos

x + 3 - 2 - x

Então vamos colocar o módulo ali

x + 3 - 2 - x = 5 , x ≥ 2 2 x + 1 , - 3 ≤ x < 2 - 5 , x < - 3

x + 3 - 2 - x = 5 , x ≥ 2 2 x + 1 , - 3 ≤ x < 2 5 , x < - 3

Juntando os intervalos de 5

x + 3 - 2 - x = 5 , x ≥ 2   o u   x < - 3 2 x + 1 , - 3 ≤ x < 2 temos que abrir esse último módulo

Passo 5

Vamos abrir 2 x + 1

2 x + 1 = 2 x + 1 , 2 x + 1 ≥ 0 - 2 x + 1 , 2 x + 1 < 0

Resolvendo aquela inequação, vamos ter

2 x + 1 ≥ 0

x ≥ - 1 2

E

2 x + 1 < 0

x < - 1 2

Resultando em

2 x + 1 = 2 x + 1 , x ≥ - 1 2 - 2 x - 1 , x < - 1 2

Passo 6

Finalmente, chegamos no último módulo

x + 3 - 2 - x = 5 , x ≥ 2   o u   x < - 3 2 x + 1 , x ≥ - 1 2 - 2 x - 1 , x < - 1 2 , - 3 ≤ x < 2 Que vai ficar

x + 3 - 2 - x = 5 , x ≥ 2   o u   x < - 3 2 x + 1 , - 3 ≤ x < 2   e   x ≥ - 1 2 - 2 x - 1 , - 3 ≤ x < 2   e   x < - 1 2

Arrumando os intervalos

x + 3 - 2 - x = 5 , x ≥ 2   o u   x < - 3 2 x + 1 , - 1 2 ≤ x < 2   - 2 x - 1 , - 3 ≤ x < - 1 2

Temos 3 inequações, uma para cada intervalo

Passo 7

Com x ≥ 2   o u   x < - 3

5 = 4

Isso não vai rolar nunca né? Então não temos solução nesse intervalo

Passo 8

Com - 1 2 ≤ x < 2

2 x + 1 = 4

2 x = 4 - 1

2 x = 3

x = 3 2

Esse valor está no intervalo, então

x 1 = 3 2

Passo 9

Com - 3 ≤ x < - 1 2

- 2 x - 1 = 4

- 2 x = 4 + 1

- 2 x = 5

x = 5 - 2

x = - 5 2

Esse valor está no intervalo, então

x 2 = - 5 2

Resposta

x 1 = 3 2

x 2 = - 5 2

Exercícios de Livros Relacionados

Resolva as equações.|2 x + 3| = 0
Prove:|x + y| = |x| + |y| harr x y = 0
Resolva as equações.|x + 1| = 3
5 - Elimine o módulo.d) |x| + |x - 1| + |x - 2|
Resolva as equações.|x + 1| = 3