Exercícios Resolvidos de Equação modular

Enunciado

Como o termo dentro do módulo é igual ao cara fora do módulo, ignorando aquele sinal. Vamos fazer essa equação pela definição de módulo

Precisamos analisar o sinal daquela função de grau.

Ela vai ser uma parábola, com o , então o gráfico vai ser algo assim

Resta olharmos onde estão as raízes

Então teremos

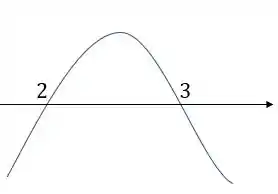
Assim, ela vai ser positiva quando estiver entre e e negativa no resto

Assim, vamos ter duas equações

Resolvendo a primeira, vamos ter

Dividindo por

Essa é aquela equação que achamos no passo anterior, então vamos ter

Que é são valores que estão naquele intervalo do

Na segunda equação, vamos ter

Mas aqui nem temos equação, porque os dois lados são rigorosamente iguais. Isso nos diz que a solução disso é todo o intervalo

Juntando as duas respostas

Temos que a solução vai ser