Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Espalhamento Compton

Ver Teoria
Exercício 1012345678911121314151617181920212223242526272829303132333435363738394041424344454647

Enunciado

Origens da Teoria Quântica

Considere um fóton de energia E γ que colide com um elétron em repouso.

A radiação desviada é observada formando um ângulo θ com a direção da radiação incidente, o eixo X .

Dê as suas respostas em função das constantes h , c . Da massa de repouso do elétron m 0 e , de E γ e de θ .

  1. Qual o comprimento de onda e a energia da radiação espalhada?
  2. Qual o vetor momento linear da radiação espalhada?
  3. Qual o vetor momento linear do elétron espalhado?
  4. Qual a energia total do elétron espalhado?

Passo 1

Trata-se de um problema de espalhamento, o que acontece é algo desse tipo:

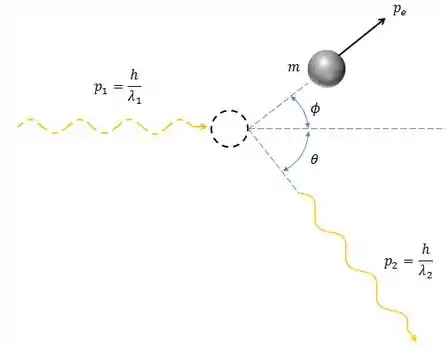
Passo 2

Letra (a): Qual o comprimento de onda e a energia da radiação espalhada?

De acordo com Compton, os comprimentos de onda da radiação incidente λ 1 e da radiação espalhada λ 2 estão relacionados por:

λ 2 - λ 1 = h m c   1 - cos ⁡ θ

Assim:

λ 2 = λ 1 + h m 0 e c 1 - cos ⁡ θ

Podemos relacionar a energia da radiação incidente E γ com λ 1 a partir de:

E γ = h f 1 = h c λ 1

λ 1 = h c E γ

Por fim, o comprimento de onda da radiação espalhada é dada por:

λ 2 = h c E γ + h m 0 e c 1 - cos ⁡ θ

Passo 3

A energia da radiação espalhada E ' γ é relacionada com o seu comprimento de onda λ 2 a partir de:

E γ ' = h c λ 2

E γ ' = h c h c E γ + h m 0 e c 1 - cos ⁡ θ = 1 1 E γ + 1 m 0 e c 2 1 - cos ⁡ θ

Passo 4

Letra (b): Qual o vetor momento linear da radiação espalhada?

O momento linear da radiação espalhada é dado por:

p = E c = h f c = h λ

Logo:

p = E γ ' c = 1 c E γ + 1 m 0 e c 1 - cos ⁡ θ

Como a radiação desviada faz um ângulo θ com o eixo X, podemos dizer que:

p x = p cos ⁡ θ = cos ⁡ θ c E γ + 1 m 0 e c 1 - cos ⁡ θ

p y = p sen ⁡ θ = sen ⁡ θ c E γ + 1 m 0 e c 1 - cos ⁡ θ

Portanto, o vetor momento linear da radiação espalhada é dada por:

p → = cos ⁡ θ c E γ + 1 m 0 e c 1 - cos ⁡ θ i ^ + sen ⁡ θ c E γ + 1 m 0 e c 1 - cos ⁡ θ j ^

Passo 5

Letra (c): Qual o vetor momento linear do elétron espalhado?

p e → = p 1 → - p 2 →

Onde:

p 1 → = E γ c i ^

p 2 → = cos ⁡ θ c E γ + 1 m 0 e c 1 - cos ⁡ θ i ^ + sen ⁡ θ c E γ + 1 m 0 e c 1 - cos ⁡ θ j ^

Assim, o vetor momento linear do elétron espalhado é dado por:

p e → = E γ c - cos ⁡ θ c E γ + 1 m 0 e c 1 - cos ⁡ θ i ^ - sen ⁡ θ c E γ + 1 m 0 e c 1 - cos ⁡ θ j ^

Passo 6

Letra (d): Qual a energia total do elétron espalhado?

Partindo do princípio da conservação de energia, a energia total do sistema antes da colisão deve ser igual à energia total do sistema após a colisão:

E a n t e s = E a p ó s

E γ + E 0 = E e + E γ '

E e = E γ - E γ ' + E 0  

Onde:

E γ ' = 1 1 E γ + 1 m 0 e c 2 1 - cos ⁡ θ

E 0 = m 0 e c 2

Portanto:

E e = E γ - 1 1 E γ + 1 m 0 e c 2 1 - cos ⁡ θ + m 0 e c 2

Resposta

Letra (a):

λ 2 = h c E γ + h m c 1 - cos ⁡ θ

E γ ' = h c h c E γ + h m 0 e c 1 - cos ⁡ θ = 1 1 E γ + 1 m 0 e c 2 1 - cos ⁡ θ

Letra (b):

p → = cos ⁡ θ c E γ + 1 m c 1 - cos ⁡ θ i ^ + sen ⁡ θ c E γ + 1 m c 1 - cos ⁡ θ j ^

Letra (c):

p e → = E γ c - cos ⁡ θ c E γ + 1 m 0 e c 1 - cos ⁡ θ i ^ - sen ⁡ θ c E γ + 1 m 0 e c 1 - cos ⁡ θ j ^

Letra (d):

E e = E γ - 1 1 E γ + 1 m 0 e c 2 1 - cos ⁡ θ + m 0 e c 2

Exercícios de Livros Relacionados

Um fóton incidente de energia Ei sofre espalhamento de Compton no ângulo de θ. Mostre que a energia Es do fóton espalhado é dada por E s = E i 1 + E i m e c 2 1 - cos ⁡ θ
Quando os fótons são dispersos por elétrons em uma amostra de carbono, a mudança no comprimento de onda é de 0,33 pm. Encontre o ângulo de dispersão. (Suponha que os elétrons estejam se movendo inicia
Durante um laboratório de física avançada, os alunos usam raios X para medir o comprimento de onda de Compton, λC. Os alunos obtêm os seguintes desvios de comprimento de onda λ2 - λ1 em função do ângu
Encontre a mudança no comprimento de onda dos fótons dispersos por elétrons estacionários livres em θ = 60 °. (Suponha que os elétrons estejam se movendo inicialmente a uma velocidade desprezível e es
Os fótons em um feixe monocromático são espalhados por elétrons. O comprimento de onda dos fótons dispersos em um ângulo de 135 ° com a direção do feixe de fótons incidentes é 2,3% menor que o comprim