É realizado um experimento onde fótons são espalhados por elétrons livres inicialmente em repouso. Verifica-se que: (1) os fótons emergem em relativamente à direção de incidência; (2) os elétrons espalhados são completamente freados por uma diferença de potencial V.
(a) Escreva as expressões para as conservações de energia e de momento linear para o processo. Denomine: o comprimento de onda do fóton espalhado; o comprimento de onda do fóton incidente, o ângulo entre o elétron espalhado e a direção de incidência do fóton; o vetor momento linear do elétron espalhado e a energia cinética do elétron espalhado.
(b) Qual o comprimento de onda dos fótons incidentes? Forneça a sua resposta em função da diferença de potencial V e do comprimento de onda Compton .
(c) Qual o comprimento de onda dos elétrons espalhados? Forneça sua resposta em função do comprimento de onda dos fótons incidentes e do comprimento de onda Compton
Passo 1
(a) Vamos esquematizar o que está acontecendo já colocando as incógnitas como foi pedido no item (a):
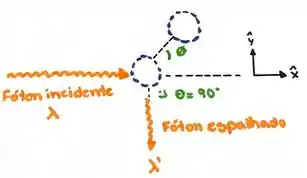
Vamos começar fazendo a conservação da energia.
Antes da colisão, como o elétron está parado, temos somente a energia do fóton, dada por:
Depois da colisão, temos a energia do fóton espalhado e a energia cinética do elétron:
Igualando a energia antes e depois:
Para fazer a conservação do vetor momento linear, vamos fazer a conservação da sua componente x e da sua componente y.
Começando pela componente x, antes da colisão temos momento linear somente devido ao próton incidente, já que o elétron se encontra parado.
Esse momento pode ser escrito então como:
Depois da colisão, na direção x, temos momento linear somente devido ao elétron:
Igualando:
Agora para a direção y, antes da colisão não temos momento linear nessa direção:
Depois da colisão, temos momento em y devido ao elétron e ao fóton espalhado:
Igualando:
Passo 2
(b) Como o enunciado diz que a diferença de potencial freia o elétron, podemos escrever:
Substituindo na equação da conservação de energia:
Dividindo os dois lados por hc:
Pela equação do efeito Compton:
Como
Queremos a resposta em função apenas de V e , então vamos substituir pelo que achamos antes:
Dividindo por eV:
Que é uma equação do segundo grau em
A única resposta possível ( deve ser positivo) vai ser:
Passo 3
(c) Para calcular o comprimento de onda do elétron espalhado, vamos usar o comprimento de onda de de Broglie:
Pela conservação do momento em x:
Pela conservação do momento em y:
Usando que:
E substituindo os valores de e encontrados nessa equação, vamos ter:
Substituindo:
Vamos ter:
Colocando pra fora no denominador e simplificando:
Resposta
(a) Conservação de energia:
Conservação do momento linear em x:
Conservação do momento linear em y:
(b)
(c)