Numa experiência de espalhamento de raios por um alvo de grafite (efeito Compton) verifica-se que a intensidade dos raios espalhados num ângulo , medido a partir da direção de incidência, em função do comprimento de onda é dada pela curva abaixo, onde e .
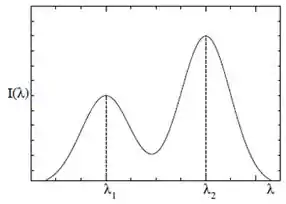
- Qual é o comprimento de onda dos raios incidentes? Justifique.
- Calcule o ângulo de espalhamento .
- Deduza a fórmula para a energia cinética do elétron no espalhamento em função de , , e ?
- Qual seria a equação para se os raios fossem espalhados por prótons em repouso ao invés de elétrons?
Passo 1
Letra a)
No espalhamento Compton, o comprimento de onda da luz após colidir com o elétron aumenta. Assim, entre os dois picos, o comprimento de onda dos raios X incidentes vai ser o menor dentre ambos.
Passo 2
Letra b)
A variação do comprimento de onda é dada por:
Rearrumando:
Do enunciado
- O feixe de raio X incide em elétrons, sendo o comprimenta de onda Compton
- A diferença entre os comprimentos de onda é
Logo, temos .
Passo 3
Letra c)
Da conservação da energia, temos:
A variação da energia do elétron se deve apenas pelo seu ganho de energia cinética (pois antes o consideramos como em repouso).
Na equação da conservação da energia ficamos com
A energia de um fóton é:
Ou seja:
Passo 4
Letra d)
Se os fótons do raio X fossem espalhados por prótons, teríamos:
Onde é a massa do próton e definimos é o comprimento de onda Compton do próton.
Resposta
Letra a)
Letra b)
Letra c)
Letra d)