Espalhamento de Compton.
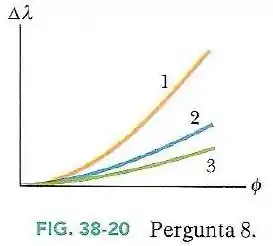
A Fig.38-20 mostra o deslocamento de Compton em função do ângulo de espalhamento para três diferentes partículas estacionárias usadas como alvo.
Coloque as partículas na ordem de suas massas, começando pela maior.
Passo 1
O deslocamento de Compton em função do ângulo de espalhamento é dado por:
De até , o cosseno varia de até , fazendo o deslocamento aumentar a medida que o ângulo de espalhamento aumenta.
A medida de o quanto o ângulo de espalhamento afeta o deslocamento de Compton é dado pelo comprimento de onda de Compton da partícula:
Quanto maior o comprimento de onda de Compton mais o deslocamento aumenta com o ângulo.
Assim, pelo gráfico, temos:
Passo 2
O comprimento de onda de Compton é inversamente proporcional à massa da partícula.
Quanto maior esse valor, menor é a massa da partícula. Logo:
Começando pela maior, a ordem das massas das partículas é: