Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Espalhamento Compton

Ver Teoria
Exercício 1412345678910111213151617181920212223242526272829303132333435363738394041424344454647

Enunciado

Origem do Exercício

Num espalhamento Compton, um fóton de comprimento de onda λ 0 incide em um elétron inicialmente em repouso (massa m 0 ). O fóton espalhado é observado numa direção que faz um ângulo de 60 ° em relação à direção de incidência.

As respostas devem ser dadas em termos de λ 0 , m 0 , h e c .

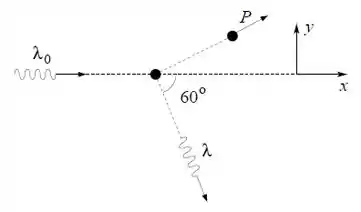
  1. Determine o comprimento de onda λ do fóton espalhado.
  2. Calcule a energia cinética do elétron após a colisão.
  3. Calcule a componente P y do momento linear do elétron após a colisão.

Passo 1

Letra a)

O deslocamento Compton sofrido pelo fóton espalhado é

Δ λ = λ - λ 0 = h m 0 c ∙ 1 - cos ⁡ θ

Como o ângulo de espalhamento é θ = 60 ° , então cos ⁡ θ = 1 / 2 e 1 - cos ⁡ θ = 1 / 2 .

Logo, o comprimento de onda do fóton espalhado será:

λ = λ 0 + h 2 m 0 c

Passo 2

Letra b)

A energia cinética do elétron vai ser igual a energia perdida pelo fóton.

A energia do fóton incidente é:

E i n c = h f 0 = h c λ 0

A energia do fóton espalhado:

E e s p = h f = h c λ = h c λ 0 + h 2 m 0 c

Fazendo a diferença:

K = h c λ 0 - h c λ 0 + h 2 m 0 c

Passo 3

Letra c)

Pela conservação do momento linear a componente P y do momento do elétron vai ser igual à componente P y ' do momento do fóton.

O momento do fóton é dado por:

p = h λ = h λ 0 + h 2 m 0 c

A componente ao longo do eixo y vai ser

P y ' = p ∙ sen ⁡ 60 ° = 3 2 p = 3 h 2 λ 0 + h m 0 c = P y

Resposta

Letra a)

λ = λ 0 + h 2 m 0 c

Letra b)

K = h c λ 0 - h c λ 0 + h 2 m 0 c

Letra c)

P y = 3 h 2 λ 0 + h m 0 c

Exercícios de Livros Relacionados

Um fóton incidente de energia Ei sofre espalhamento de Compton no ângulo de θ. Mostre que a energia Es do fóton espalhado é dada por E s = E i 1 + E i m e c 2 1 - cos ⁡ θ
Quando os fótons são dispersos por elétrons em uma amostra de carbono, a mudança no comprimento de onda é de 0,33 pm. Encontre o ângulo de dispersão. (Suponha que os elétrons estejam se movendo inicia
Durante um laboratório de física avançada, os alunos usam raios X para medir o comprimento de onda de Compton, λC. Os alunos obtêm os seguintes desvios de comprimento de onda λ2 - λ1 em função do ângu
Encontre a mudança no comprimento de onda dos fótons dispersos por elétrons estacionários livres em θ = 60 °. (Suponha que os elétrons estejam se movendo inicialmente a uma velocidade desprezível e es
Os fótons em um feixe monocromático são espalhados por elétrons. O comprimento de onda dos fótons dispersos em um ângulo de 135 ° com a direção do feixe de fótons incidentes é 2,3% menor que o comprim