Um feixe de raios X com um comprimento de onda de , no sentido positivo do , incide em um alvo que contém elétrons quase livres.
Para o espalhamento de Compton a de um fóton por um desses elétrons, determine:
- O deslocamento de Compton.
- A variação da energia do fóton.
- A energia cinética do elétron após o espalhamento.
- O ângulo entre o semi-eixo positivo e a direção de movimento do elétron após o espalhamento.
Passo 1
Letra a)
O deslocamento de Compton é dado por:
Para , temos
No caso do elétron:
E assim:
Passo 2
Letra b)
A energia inicial do fóton era de:
Onde:
- (pelo enunciado)
O comprimento de onda do fóton após a interação vai ser:
E assim sua energia será:
A variação de energia fica:
Onde o sinal negativo indica que a energia foi perdida.
Passando para , ficamos com:
Passo 3
Letra c)
Toda a energia perdida pelo fóton é absorvida pelo elétron na forma de energia cinética. Por isso a energia cinética do elétron será igual ao módulo da variação de energia do fóton.
Passo 4
Letra d)
Quando o fóton se aproxima do elétron, o elétron está parado e, por isso, não tem momento linear. Já o fóton tem um momento linear com componente apenas na direção do semi-eixo positivo.
Como o espalhamento do fóton é de , o seu momento linear final tem componente apenas na direção do semi-eixo negativo.
Por isso, o elétron adquire um momento linear apenas com componente no semi-eixo positivo.
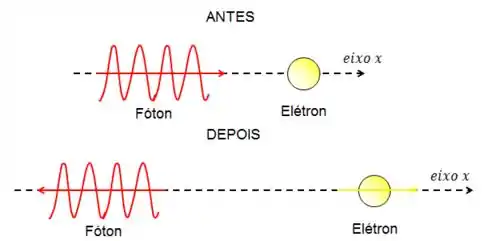
Isso significa que o ângulo entre o movimento do elétron e o semi-eixo positivo é igual a zero.
Resposta
Letra a)
Letra b)
Letra c)
Letra d)