Uma rede de transmissão em micro-ondas emite a uma frequência de , com potência de .

a) Quantos fótons são emitidos por segundo por essa rede?

b) Para um metal típico, é possível arrancar elétrons de sua superfície pela incidência direta dessas ondas? Justifique.

Para os itens (c) e (d), considere a seguinte situação:

Em um experimento Compton, onde um fóton de comprimento de onda de colide com um elétron em repouso, observa-se que o elétron ganha, após o espalhamento, uma energia cinética equivalente a de sua massa de repouso.

c) Qual é o comprimento de onda do fóton espalhado?

d) Qual é o ângulo de espalhamento do elétron, em relação a direção do fóton incidente?

Para o item (e), considere agora:

Um pósitron (anti-partícula do elétron, com mesma massa e carga oposta) viajando na direção incide sobre um elétron em repouso. O par elétron-pósitron se aniquila formando dois fótons, como mostrado na figura.

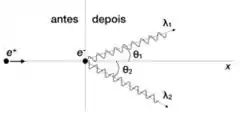
e) Mostre que, nesse caso, a “Fórmula Compton” é dada por

onde e são os comprimentos de onda dos fótons criados e é o ângulo de abertura entre suas direções ().

No item (b) queremos saber se essa radiação é suficiente para causar efeito fotoelétrico em metais, isto é, se ela capaz de ejetar elétrons dos metais. Para isso, vamos calcular a energia de um fóton:

Para ficar mais fácil fazer a comparação, vamos calcular essa energia em elétron-volt e, para isso, temos que usar :

Sabemos que as energias mínimas para ejetar elétrons dos metais são as chamadas função trabalho, que são da ordem de , ou valores próximos disso. Vemos que a energia do fóton nesse caso é bem menor que a função trabalho, de modo que essa radiação não é capaz de ejetar elétrons por efeito fotoelétrico.

Agora vamos para o item (c)!

Um fóton com comprimento de onda é espalhado quando incide sobre um elétron em repouso. O comprimento de onda do fóton espalhado é , dado por

onde e é o ângulo de espalhamento do elétron. Esse é conhecido efeito Compton.

O enunciado diz que a energia cinética do elétron após o espalhamento é equivalente a de sua massa de repouso. Portanto,

Usando a conservação da energia, temos que a energia inicial do fóton é igual a energia do fóton espalhado somada com a energia cinética do elétron:

Como , temos que

Daí, temos

Logo,

Sabemos que para o elétron e . Como , temos que

Fazendo as continhas,

Note que o comprimento de onda do fóton espalhado é maior que o do fóton incidente, de modo que sua energia é menor. Isso faz muito sentido pois o fóton perdeu parte de sua energia para o elétron!

No item (d) nós queremos o ângulo de espalhamento. Para achar isso, usamos a fórmula do espalhamento Compton:

Usando , e :

Usando uma calculadora, achamos

Se você estivesse fazendo a prova e fez os itens (c) e (d), você não precisaria fazer o item (e). Se você escolhesse fazer o item (e), não precisaria fazer os itens (c) e (d). Além disso, escolhendo o item (e) você podia até ganhar uma nota extra porque ele valia um pouco mais...

Dito isso, vamos resolver o item (e)!

Um pósitron com massa com momento inicial colide com um elétron (também de massa ) e os dois se aniquilam, dando origem a dois fótons. Antes da colisão, o momento total do sistema era:

Além disso, a energia era

Nessa última expressão, considerei as energias de repouso das duas partículas e a energia cinética do pósitron em movimento.

Depois da colisão, as partículas desaparecem e dão origem a dois fótons. A energia de cada fóton é dada por

Assim, após a colisão a energia é

Já para o momento a situação é mais complicada. Sabemos que para um fóton, o momento é

Mas não se esqueça que o momento é uma grandeza vetorial, de modo que precisamos fazer a decomposição nas direções e :

Observe que a componente do momento do fóton 2 é negativa! Com isso, o momento do sistema após a colisão era

Vamos aplicar primeiro a conservação do momento linear:

Eu sei que o natural seria igualar as componentes de cada lado da equação acima e sair com duas equações. Isso não está errado, porém resolver o problema assim dá muita conta. Vamos fazer de um jeito alternativo:

O primeiro produto escalar é trivial:

Já o segundo vai envolver uma conta interessantes:

Podemos escrever o último termos como

onde é o ângulo entre os vetores. Assim,

Com isso nós nem precisamos olhar para e , o que importa é a soma deles! Igualado os termos dos momentos antes e depois da colisão:

Lembre-se que e , de modo que

Agora vamos usar a conservação da energia:

Antes de continuar, precisamos escrever em termos de outras coisas. Para isso, vamos lembrar que

A energia cinética do pósitron é a energia total menos a energia de repouso. Mas sabemos que , de modo que

Substituindo no lado direito da equação de conservação da energia:

Assim,

Nos passos anteriores achamos duas equações:

Vamos brincar com a primeira equação. Sabemos que a energia total do pósitron e seu momento se relacionam por

Logo,

Mas , de modo que

Agora multiplique a primeira equação por e faça a substituição acima:

Na segunda equação do sistema, podemos isolar :

Com isso,

Daí substituímos isso na outra equação:

Simplificando tudo que dá para simplificar:

Fazemos a distributiva do lado esquerdo:

Portanto, a equação fica

Agora simplificamos os termos dos dois lados

Com isso, achamos

Pegando a expressão do último passo e trocando os termos de lado:

Ou ainda,

Mas sabemos que

Portanto,

Simplificando os denominadores , achamos a expressão procurada:

UFA! Deu trabalho, mas terminamos 😉!