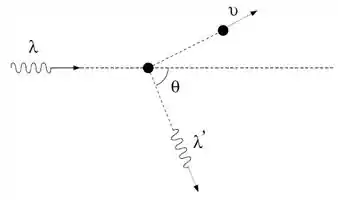
Um fóton de comprimento de onda , onde é a massa de repouso do elétron, é espalhado por um elétron em repouso. O fóton espalhado tem comprimento de onda e sua direção de propagação faz um ângulo com a direção de incidência. A energia cinética do elétron após a colisão é igual a , conforme a figura.
Nos itens abaixo forneça suas respostas em termos de , e apenas.
- Calcule o comprimento de onda do fóton espalhado.
- Calcule o ângulo de espalhamento do fóton.
- Calcule o módulo da velocidade do elétron espalhado.
Passo 1
Letra a)
Este é um problema de espalhamento Compton. Porém, como não sabemos o ângulo que o fóton faz com a direção original, não temos como usar a equação do espalhamento Compton!
Por isso, vamos seguir em outra direção.
A variação da energia do fóton é igual à energia cinética ganha pelo elétron.
Temos então:
Porém, o enunciado nos diz que .
Passo 2
Letra b)
Agora sim, a equação do espalhamento compton relaciona a diferença no comprimento de onda com o ângulo .
Os dois comprimentos de onda nós temos.
Assim, temos:
Passo 3
Letra c)
Relativisticamente, a energia cinética é dada por:
Igualando à expressão dada no enunciado.
Esse é definido como:
Assim, temos:
Resposta
Letra
Letra
Letra