10 - A figura abaixo mostra as linhas do campo eletrostático produzidas por um par de partículas de cargas q1 e q2. A figura mostra ainda duas superfícies imaginárias e fechadas, S1 e S2, indicadas pelas linhas tracejadas. A superfície S1 envolve apenas a partícula de carga q1, enquanto S2 envolve as duas partículas. Sobre essa situação, considere as afirmativas abaixo:
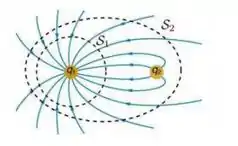
- O fluxo de campo eletrostático através de S1 vale .
- O fluxo de campo eletrostático através de S1 é negativo.
- O fluxo de campo eletrostático através de S2 é nulo.
São VERDADEIRAS as afirmativas:
- Apenas I
- Apenas II
- Apenas II
- Nenhuma delas
- I, II e III
Passo 1
Ora, o fluxo do campo elétrico dado por essa equação aqui:
Onde é o total de carga no interior da superfície fechada . Então veja que a primeira alternativa é falsa visto que S1 não envolve a carga .
Passo 2
A alternativa II é verdadeira, pois de fato as linhas de campo da carga entram na superfície S1, o que torna o fluxo negativo.
Passo 3
Ora, pela equação...
A gente percebe que o fluxo só é nulo se a carga interna for . Caso contrário não dá para saber!
Além disso, a gente consegue através do desenho
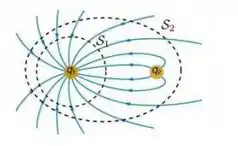
Perceber que todas as linhas de campo da carga vão para , mas existem linhas de fora vindo para também, sugerindo que é maior que em módulo, logo o fluxo não será nulo!
Resposta
Letra C.